- Title: What would a binary black hole merger look like?
- Authors: Andy Bohn, François Hébert, William Throwe, Darius Bunandar, Katherine Henriksson, Mark A. Scheel, Nicholas W. Taylor
- First author’s institution: Cornell University, Ithaca, NY
Fig. 1: A view of the Milky Way Galaxy as seen through a simulated binary black hole merger.
Astrobites discusses binary black hole mergers a lot. But what would one of these actually look like? Nothing, right? Black holes don’t emit light, they trap it. Yeah, but if there were some source of light, a flashlight or something, a backdrop of stars, then the wobbling, curving spacetime around the binary black hole (BBH) merger would become visible as distortions of the source. Remember, light rays curve around massive objects, and in this sense, black holes are lenses. What kind of lens is a BBH merger?
These authors present the first pictures of light sources lensed by BBH mergers—actually, numerical models of BBH mergers. To the right you can see what the Milky Way Galaxy would look like if a BBH merger were taking place just outside your window.
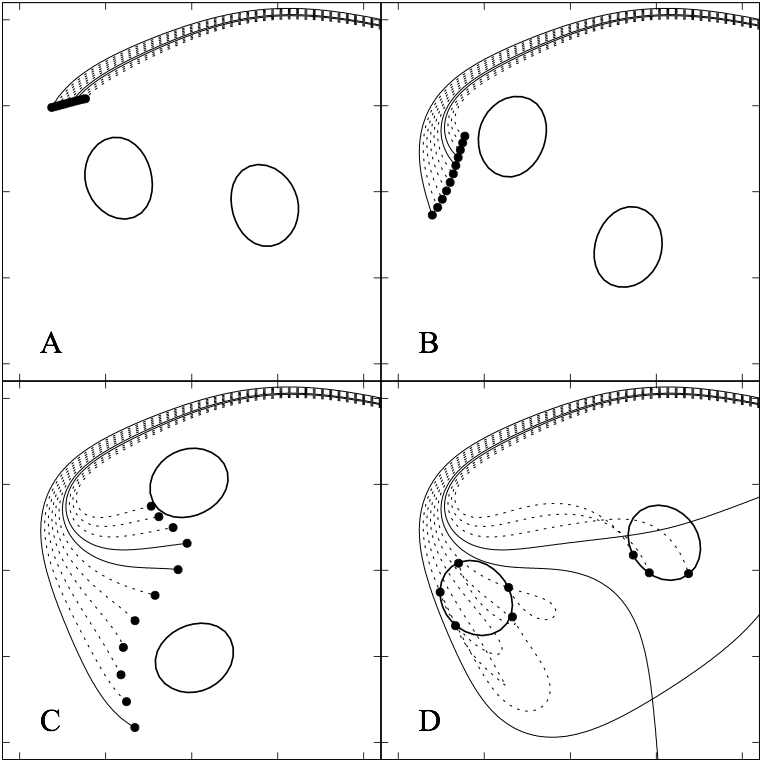
Fig. 2: Backwards-in-time trajectories of light rays through the simulated BBH merger. The ovals represent the black holes’ event horizons: surfaces of no escape. Dashed trajectories terminate in a black hole, while solid trajectories go off to spatial infinity. Because the rays are traced backwards through time, the bottom right panel shows the earliest snapshot, and ‘terminate in’ really means ‘originate from’.
To take pictures like this, pictures of their numerical models, they use a numerical pin-hole camera. A real pin-hole camera maps the angle of an incoming light ray to a unique position on the image plane. Their numerical pin-hole camera does the same in reverse: for each x,y position on the image (a pixel), it calculates the unique corresponding light ray. It traces the ray backwards in time through a previously-simulated BBH spacetime, saved as multiple snapshots of data, like a movie. Whatever the ray finally hits, that’s the pixel’s color. This is a well-known method in computer graphics, and it’s known to take a lot of computing power. Fig. 2 shows a bundle of rays traced backwards through several data snapshots.
Notice how fast the black holes are moving; the light rays barely keep up! Also notice how chaotic is the spacetime! Slight differences in initial ray trajectories yield wildly different endpoints. Clearly an accurate ray-tracing algorithm is essential to taking a true picture of their data. To this end, Bohn et al. introduce a modification to the equation describing light rays, and improve both the accuracy and the speed of their ray-tracing. Speed is important because they’re calculating hundreds of thousands of trajectories for a single picture.
Fig. 3: The background light source, painted on a sphere covering the sky.
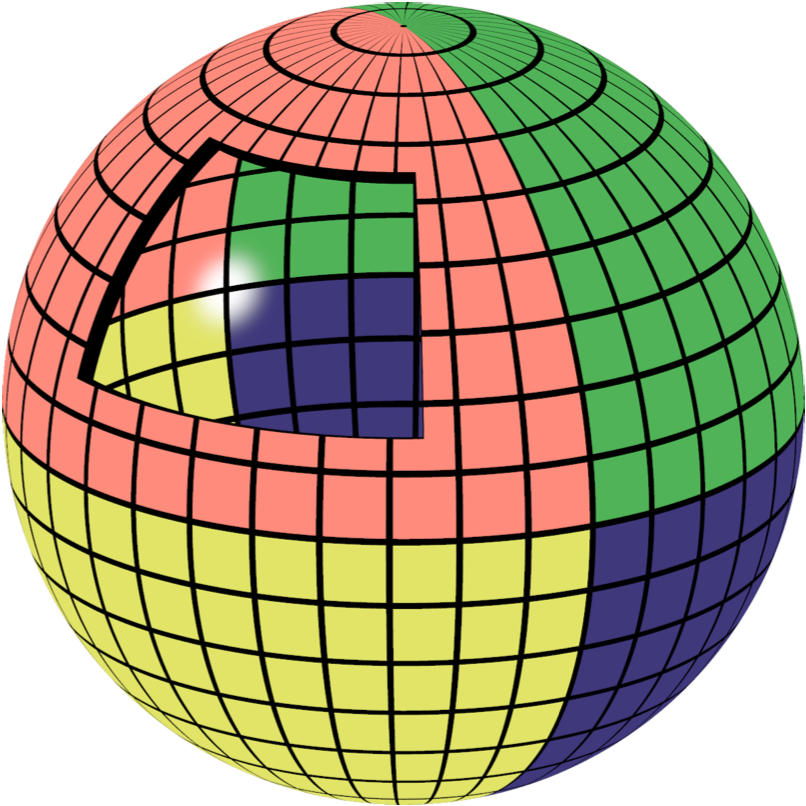
The background light source in the pictures is an artificial grid covering the entire sky, with each quarter of the sphere painted a unique color. Fig. 3 shows the sphere with a window cut out to reveal the interior. The camera and BBH merger are placed at the center, and are oriented so that the white spot is directly behind the black holes.
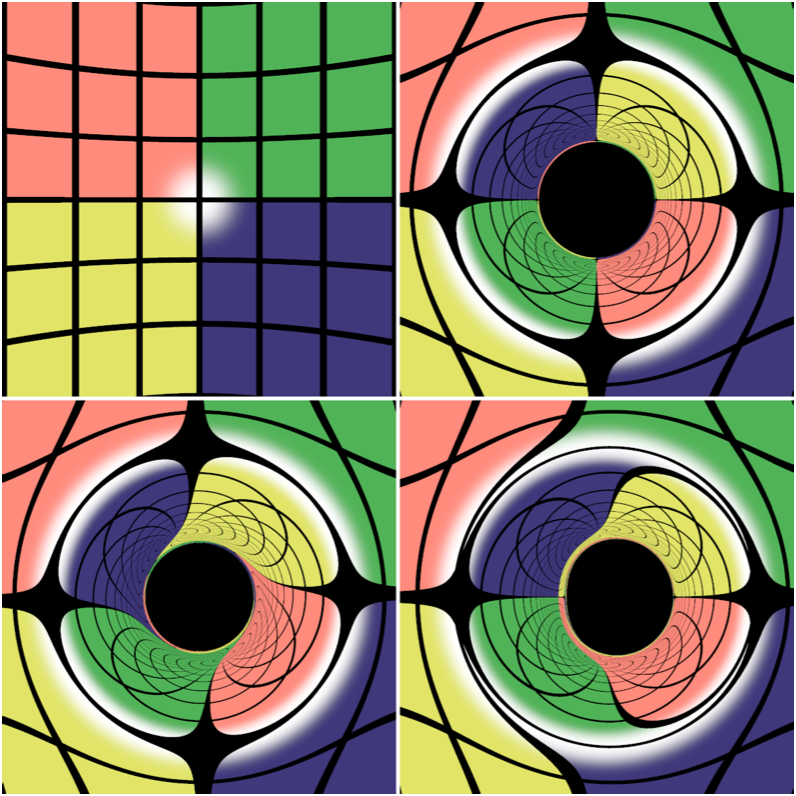
Fig. 4: Images of the inside of the artificial sphere (a) without a BH, (b) with a single nonspining BH at the center, (c) with a single spinning BH, spin axis out of the screen, (d) with the same spinning BH, spin axis up.
To get us oriented to simple black hole spacetimes, Fig. 4 shows some images of the inside of the sphere, lensed by single black holes.
Some things to explore in the figure to the left. In the lensed images (b-d) the white dot behind the black hole is transformed into a ring. This effect, called an Einstein Ring, has been well-studied. There are a number of famous examples in nature, lensed by massive galaxy clusters (1, 2, 3). The ring occurs because light rays originating from the white spot behind the BH, and passing through that ring, all get bent toward the camera by the BH. Also, in the images lensed by rotating black holes, notice the swirl in (c) and the asymmetry in (d). These effects are caused by frame-dragging, another well-studied, and verified consequence of general relativity.
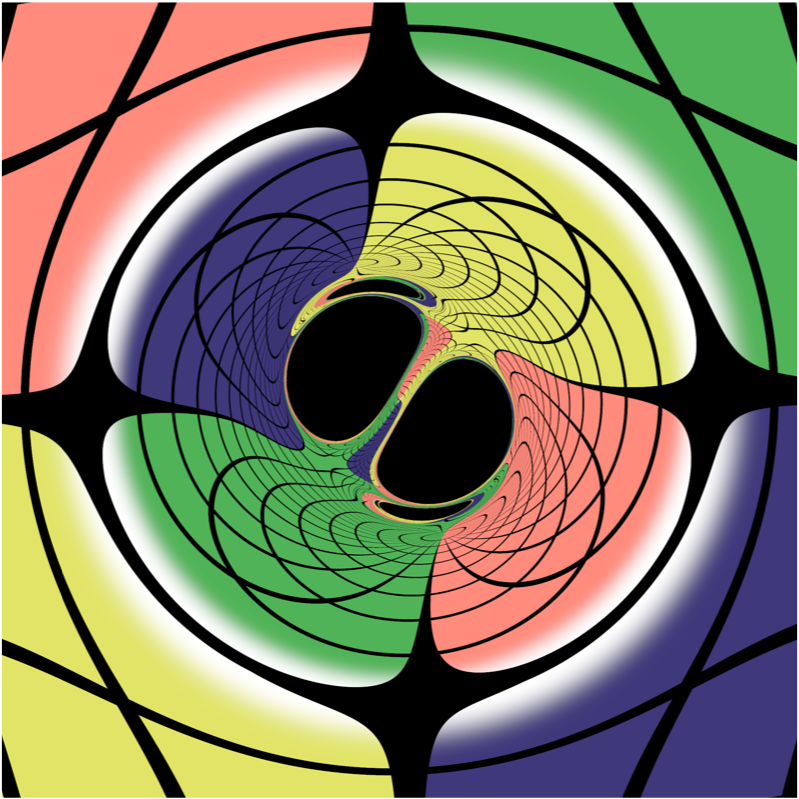
Fig. 5: An image of nonspinning, merging black holes, with the orbital angular momentum axis pointing out of the screen. You can find multiple images of each BH in this picture.
Now we’re ready to understand a picture of a BBH merger. Figs. 5 & 6 show views of the background grid lensed by two orbiting, nearly-merged, non-spinning, equal-mass black holes.
Bohn et al. point out two interesting characteristics of Figs. 5 & 6. First, out on the edge of the images, you still find an Einstein Ring. In fact, out on the edge, the effect of the orbital motion is similar to that due to a single spinning BH (in other words, Fig. 5 looks like 4c, and 6 looks like 4d). This makes sense; the frame-dragging effect is due to the angular momentum of the central masses, regardless of whether that angular momentum is due to orbital motions of two bodies, or an intrinsic spin of one body. Second, the images reveal a self-similar structure as you zoom into the edge of any of the shadows. This is because rays passing very near the BHs can take one, two, or arbitrarily many orbits around the BHs, before they fall into a BH, or escape to land on a light source. Self-similar structure is not unique to BBH spacetimes. In fact, with infinite resolution, one could in principle find infinitely many Einstein Rings around the simple BHs in Fig. 4.
Fig. 6: An image of the same black holes as in Fig. 5, with the orbital angular momentum axis pointing up. Again, you can find multiple images of each BH in this picture. The inset zooms into the image near one of the BH borders. The further one zooms, the more self-similar images of the black holes appear as thin pancake-shadows.
Can the rich structure near the merger actually be seen in nature? Probably not. Real background light sources, like those in Fig. 1, obscure the self-similarity revealed by the continuous light source used in this work. (Although, if you look closely you can find several star patterns repeated in Fig. 1.) Furthermore, stellar-mass BBH mergers go through their final orbits in only a few milliseconds. And finally, perhaps most significantly, telescopes are fundamentally limited in their ability to resolve differences across small angular separations. This means only very nearby mergers could potentially be imaged. How nearby depends on the observing wavelength and the size of the telescope. Nevertheless, the authors point out that similar lensing anomalies may be visible as overall brightness variations in a merger involving light-emitting matter, like a neutron star.
There’s a mathematical beauty and richness in the images calculated and presented here by Bohn et al. And they’re really happening out there. It’s somehow humbling and wonderful to know that though these effects may exist, they will probably never be seen. There’s a poem by Wendell Berry that begins with a quote from his daughter: “I hope there’s an animal somewhere that nobody has ever seen. And I hope nobody ever sees it.”
Full disclosure: this Astrobites author collaborates with Bohn et al. and thinks they’re swell.
Addendum (added 11.7.14): Check out these movies of mergers, posted online after this astrobites was written.
