- A Novel Method for identifying Exoplanetary Rings
- Authors: J. I. Zuluaga, D. M. Kipping, M. Sucerquia and J. A. Alvarado
- First Author’s Institutions: 1) Harvard-Smithsonian Center for Astrophysics, 2) FACom – Instituto de Fisica – FCEN, Universidad de Antioquia, Colombia, 3) Fulbright Visitor Scholar
Today’s question: Do you like rings?
Let’s start this Astrobite a bit different than usual. Before you read on, please click here and tell us about your favorite planet… Are you done? Good! The reason why I’m asking has to do with the ring structure around Saturn. Assuming you like Saturn’s rings, you are probably also curious whether exoplanets reveal ring structures, too, and how those can be detected. The answer to the first question is ‘Yes!’ and if you like Saturn, you probably fell in love with this planet. As Ruth told you, the authors put a lot of work into finding an explanation for the observed profile by comparing different transit profiles before they concluded that the planet hosts circumplanetary rings. That’s the point where today’s authors come into play. They present a model, which simplifies the detection of exorings.
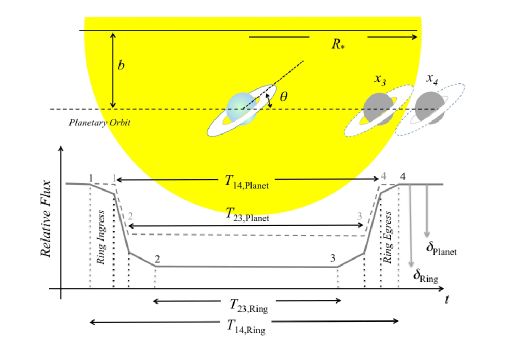
Figure 1: Sketch of a transit of a planet with rings (top) and the corresponding schematic illustration of the observed flux (bottom). corresponds to the entire transiting interval of the planet with/without rings, while
corresponds to the time interval of the full transit of the planet with/without rings. The figure corresponds to Fig. 1 in the letter.
Characteristic features of planets hosting circumplanetary rings
Figure 1 illustrates their underlying thoughts. The yellow area represents the host star and I guess it is easy to spot the planet with its circumplanetary rings moving from left to right. When the planet moves together with the rings to the right of position (when it starts its egress), one side of the rings will not hide the light of the host star anymore and thus the observed flux from the host star slowly increases. The planet itself leaves the transiting area a bit later, which then leads to a steeper increase in flux until the planet does not hide any of the light anymore. At that point the increase in flux is shallower again due to the other side of the ring structure, which still covers part of the light from the host star before this side also stops transiting at position
. When the planet and its rings start transiting (the ingress), the process is reversed. The illuminating area of the star gets more hidden and the flux decreases. Principally there are two different intervals for a transit of a planet:
- The time from the entering of the planet in the transiting region until the time the planet does not cover any light of the host anymore (corresponding to
or just “transit”).
- The time in which the entire planet covers the light of the host (corresponding to
or “full transit”).
Considering now also the rings, four time intervals exist, namely ,
,
and
(as shown in the graph of Fig. 1). The relative flux difference during the transit of the planet with and without the rings compared to the unperturbed flux of the star is called transit depth (
. In practice, the slopes corresponding to the ingress/egress of the ring and the ingress/egress of the planet are difficult to distinguish from each other. The authors stress that exoplanets with rings could be mistakenly interpreted as ringless planets. Assuming the star and the planet as being spherical and a uniform shape of the rings, the transit depth simply becomes the ratio of the area hidden by the planet including the rings and the projected surface area of the star (
). If the rings’ plane is orientated perpendicular to the line of sight and the observed transit depth of the ring is interpreted as the transit depth of a ringless planet, the overestimated radius of the planet leads to an underestimation of the planetary density (as shown in Fig. 2).
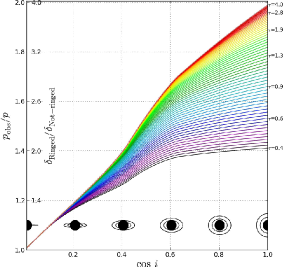
Figure 2: Illustration of the effect of the projected inclination of the of the rings on the ratio of observed to true planetary ratio. The degree of inclination is illustrated by the black dots and their surrounding rings. The different colours represent different transit depths. The figure corresponds to the upper panel in Fig. 2 of the letter.
Additionally, the authors repeat the derivation that stellar density is proportional to
reveals another potential misinterpretation. Figure 3 illustrates the effect on stellar density of different ring inclinations. In the case of a ring plane perpendicular to the orbital direction, the stellar density would be overestimated. However, in the more common case of alignment of the rings’ plane with the orbiting plane, the increased difference
leads to an underestimation of the stellar density.
A publicly available code allows for hunting
Taking into account the described phenomena of anomalous depth and the photo-ring effect to estimate probability distribution functions for the occurrence of the effects, the authors developed a computer code, which you can use to go out hunting for exoring candidates! They suggest that you focus on planets (candidates) with low densities and use their publicly available code (http://github.org/facom/exorings) to do so. But here’s a disclaimer: The code can only find candidates. To confirm their existence you still need to do a complex fit of the light curve. That’s something the code cannot do for you.

Figure 3: Illustration of the photo-ring effect. The color scale displays the relative difference of observed radiation to stellar radiation. The two axis represent the tilt of the rings with respect to the two planets. Note that the y-axis corresponds to the actual angle, while the projected inclination on the x-axis is a cosine. The black crosses represent a sub-sample of observed transits with low obliquity. The figure corresponds to the upper panel of Fig. 3 in the letter.




Very neat. It would be cool if this idea were eventually crowd-sourced! Maybe a game could be designed to hunt for exo-rings.
Hi! I was wondering exactly how we derived the dependence of stellar density on these transit times… it seems non-intuitive. Is it from some kind of Keplerian law?
HI Zoey, Seager and Mallen-Ornealas showed how to do this using Kepler’s third law (2003, ApJ, 585, 1038). The best explanation of this comes from pages 2 & 3 in Kippings 2014 paper Characterizing Distant Worlds with Asterodensity
Profiling (MNRAS, 440, 2164). Once you translate Kepler’s third law into the terms which you can back out of a transit light curve it turns out to be a simple and elegant solution (with several idealized assumptions).
Great post! I know that limb darkening can also cause fluxes during ingress/egress to decrease/increase more smoothly, so is there some method of distinguishing the effects of limb darkening and the effects of rings on the transit?
I know that observationally rings have been hard to find and demonstrate (hence the interest in the paper), I was wondering if there are models of planet formation that might predict how common rings in fact are. Bascally, are rings common and are just hard to detect, or rare finds?
In practice does the difference the rings make in the observed flux really matter enough (especially compared to the uncertainty in the measurement) to substantially change things?
Also, there is a shameful lack of votes for Venus in that poll. Just saying.
Very cool!! The light curve definitely seems intuitive. Is there a way to determine the density of the ring(s) and therefore the makeup of the rings (i.e. rocks vs ice)?
I’m not familiar with the precise composition of rings, but how much of a difference would rings of different composition and makeup cause? Is there something to be accounted for there?
Are there any current theoretically or observationally determined estimates on the occurrence rate of circumplanetary rings? I think having the public search for candidates is a great idea, but I would like to know how likely one would be to find an exoring.
Not to date I think. The topic is still too “hot”. But I am sure people are working something out at the moment. 😉
This is a great way to find exorings. It would be interesting to know how much of a factor a planets exorings could potentially have on our estimates of the star and planet masses. Because of error propagation through the calculations from the light curve, I can imagine that not knowing exorings are involved could affect these estimates.
I wonder with what kind of precision is required to resolve these ring effects, granted the planet must be very close and the radii ratio must be quite large. So finding rings must be rare.
The article you link to on J1407b is incredibly cool — I love the artist’s rendering of J1407b’s rings around Saturn as seen from Earth.
How common do we think exoring planets are? Is it likely that many of the candidates are truly exoplanets with rings?
Fortunately, I recently had the chance to listen to a talk of Matt Kenworthy . He said that since they had this idea about such exorings to be the cause for those weird patterns in transit light curves they actually start to see this “more and more” in old data archives. So maybe these phenomena occur much more often than we think and may be the source behind odd looking light curves.