Authors: Kevin J. Zahnle and David C. Catling
First author’s institution: NASA Ames Research Center, USA
Status: Posted to arXiv (2017) [open access]
Escaping from prison is hard. First, you have to convince your skeptical friend to smuggle you a rock hammer and a big poster of Rita Hayworth. Then you have to spend 20 years digging a tunnel through your cell wall by night and laundering money for your despotic warden by day. You’re not even done after you crawl half a mile through a sewer pipe to break out, because you have to hike into the cornfields in a business suit to leave an inspirational note under a rock for your friend.
Escaping from Earth, on the other hand, is easy. All you have to do is go up at 25,000 miles per hour. Admittedly, that’s challenging when you’re heavy, like an Atlas V rocket, because it takes a lot of energy to make a heavy thing go fast. But when you’re light, like a hydrogen molecule, even a little jolt of energy from a ray of sunlight can free you from Earth’s gravity.
For a planet, therefore, hanging on to an atmosphere becomes a somewhat delicate proposition. Being very massive helps, because it means that the planet’s gravity is stronger, so atmosphere molecules have to reach higher speeds to escape it. Being farther away from the star helps, too, because the starlight which reaches the planet is dimmer and less able to evaporate the atmosphere.
So what separates planets that successfully hang on to atmospheres from planets that don’t? And are the planets in our own Solar System, both “atmosphered” and not, a good guide to planets beyond?
Drawing a line in the sand
The authors start by taking every big object in the solar system–planets, dwarf planets, moons, asteroids–and plotting, very colorfully, the energy it receives from the Sun (“insolation”) against the strength of its gravity. They measure gravity strength by the speed you’d have to reach to escape from the planet (“escape velocity”).
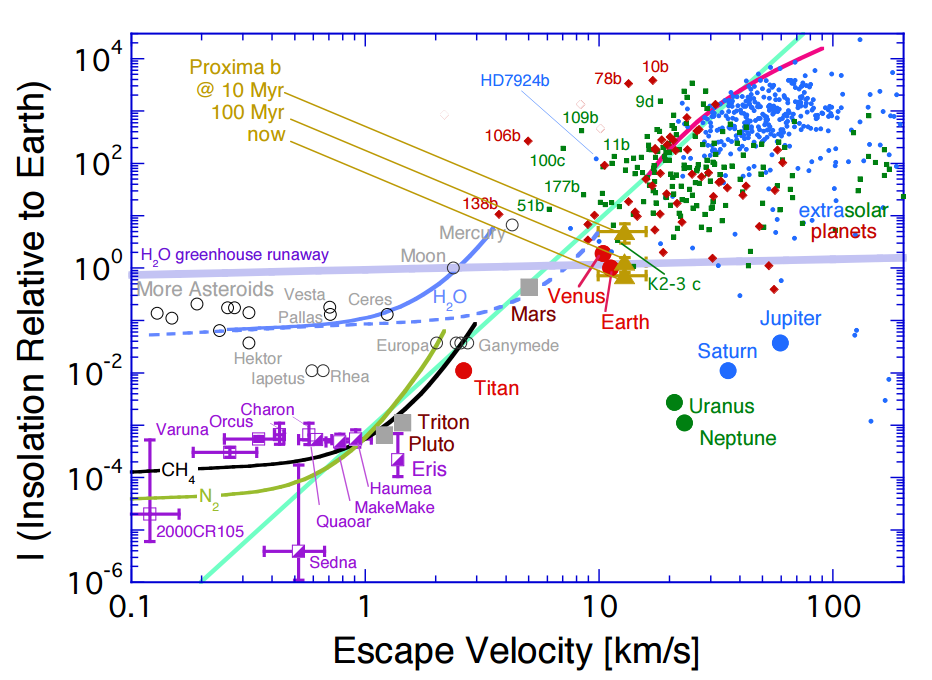
Figure 1: “Insolation” (energy received from starlight) vs. “escape velocity” (the speed at which you’d have to travel to escape the object’s gravity). The color-coding marks objects belonging to the same mass category (Saturn-sized, Neptune-sized, Earth-sized, dwarf-planet-sized, asteroid-sized). The turquoise line is the “cosmic shoreline.” (You can ignore the non-turquoise lines, which get into details about the chemical makeup of various atmospheres.)
The first thing to notice is that the objects with atmospheres (the filled-in symbols: Earth, Jupiter, Neptune, Pluto, Titan, etc.) separate surprisingly neatly from those without (the hollow symbols: Mercury, the Moon, the asteroids, etc.). The authors draw a nice turquoise line, which they term the “cosmic shoreline,” to mark the boundary, and then they draw a bunch of other lines because they hate your eyes.
This tidy cosmic shoreline is just something the authors noticed, not a fit to the data, but it hints that the authors may be on to something. If a planet’s ability to hang on to an atmosphere (or not!) depended on the amount of atmosphere it was born with, or the amount of gas deposited onto it by comets crashing into it, then insolation and escape velocity wouldn’t tell us much at all. But they do, which means that the strength of a planet’s gravity and the amount of energy it receives from its star really are determining factors.
Hanging out on the beach
Next, the authors take every exoplanet in the universe of which we’ve measured the escape velocity and toss those on the plot as well. (There are relatively few of these, even though we’ve discovered thousands of exoplanets, because measuring the escape velocity is difficult–it requires a measurement of mass and an independent measurement of size.) We can’t yet observe most of these exoplanets in enough detail to know what their atmospheres are like, but we deduce that they do have atmospheres, because their masses and sizes are consistent with the gas giants of the Solar System.
To their surprise, they find that the exoplanets more or less fall on the cosmic shoreline. This is weird because they have to extrapolate the shoreline quite a ways up and to the right to get to the exoplanets. All the exoplanets fall in the upper right corner because big exoplanets (high escape velocity) orbiting close to their host stars (high insolation) are the easiest ones to discover, so they’re the ones we’ve found and studied so far.
Once these big, hot exoplanets are added, the cosmic shoreline runs from the tiny icy bodies of the Solar System to the hot Jupiters, a hundred million times more insolated. That’s a lot of real estate for one trend to cover–it’s a simplistic picture, but an intriguing one nonetheless.
If we trust the cosmic shoreline, it might have major implications for exoplanet exploration: Proxima b, our nearest exoplanet neighbor, is right on the beach with the other atmosphered planets. A cosmic Zihuatanejo?
Featured image via Wikimedia Commons.




Can you give a simple answer to a simple person. Given an adequate power source would it be possible to leave earth and travel to the moon much slower – say, 30 mph? I appreciate you would not enter orbit about the earth, and the moon might be travelling too fast to land; but could you get there?
Yes, it would be possible! Earth’s escape velocity (~25,000 mph) is how fast you need to be going to escape Earth’s gravity without applying any additional force to keep you going. You could, in principle, leave Earth at 30 mph, but you’d need another force to continually push against the pull of gravity as you went. This is actually how rockets work, just at higher speeds! They don’t need to reach 25,000 mph, because they’re constantly being propelled forward against gravity by burning rocket fuel and expelling the byproducts.
A little molecule of atmosphere, though, doesn’t have a rocket engine (or any other means of acting against gravity), so it needs to get all the way to escape velocity.
This was the first mathematical exercise given to us students at the University of Arizona in 1961. We considered average temperature as important as well – average Brownian movement before the “jolt of energy” – solar wind? To those factors has been added re-supply ( isostasy, plate tectonics, eg. volcanoes) and strength of the planet’s magnetic field.
Yes, temperature is the main thing! At a given temperature, atmosphere molecules follow a Maxwell-Boltzmann distribution of velocities. The particles in the high-velocity, high-energy tail of that distribution are the ones that can escape–a higher temperature stretches the whole distribution toward higher velocities, so more particles can escape.
Collisions between solar wind particles and atmosphere molecules can impart enough energy to individual atmosphere molecules to get them to escape velocity. But as you say, the importance of these collisions to the atmosphere’s ultimate fate depends on the strength of the planet’s magnetic field.