Authors: Floor S. Broekgaarden et al.
First Author’s Institution: Anton Pannekoek Institute for Astronomy, University of Amsterdam, Amsterdam, The Netherlands
Status: Submitted to MNRAS, closed access
Modern astronomy relies heavily on computational resources. This is especially true when it comes to the budding field of gravitational waves. While only a handful of detections have been made to date, this number will likely grow significantly in the coming years. By comparing the observed properties and frequency of gravitational wave events with simulations, astronomers can test their theories about the origin of certain objects. However, getting good results from simulations requires a lot of computational time. The authors of today’s paper came up with a way to speed up the computational efficiency and increase the accuracy of simulations using an algorithm called STROOPWAFEL (Simulating The Rare Outcomes Of Populations With AIS For Efficient Learning).
Simulating Gravitational Wave Systems
Gravitational waves that are large enough for us to detect come from “Double Compact Object” (DCO) mergers. When stars die, some of them become compact objects like neutron stars or black holes. Some stars are originally in a binary system, with two stars orbiting around each other. In rare cases, when these stars die they can form a DCO, with either two neutron stars, two black holes, or a neutron star and a black hole in orbit. Sometimes, these objects will merge and in the process give off gravitational waves.
The chance of an arbitrary binary star system evolving into an object that will give off gravitational waves is extremely rare. Even rarer to find is a subset of DCO mergers, like two neutron stars, that will also give off visible light. Before the implementation of STROOPWAFEL, a large number of simulations would have to be run over a large parameter space for the initial conditions of the binary star system. Even with millions of simulated binary systems, there is a poor sampling of subsets of rare events.
STROOPWAFEL
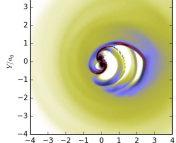
Enter STROOPWAFEL, an algorithm which helps determine which set of initial parameters (like mass of stars and orbital distance) are more likely to result in an event specified by the user. After choosing the desired outcome, like a DCO merger, the code decides which parameters to run through a binary star simulation code and gets better at guessing parameters as time goes on. The authors describe how their algorithm works like the classic game Battleship. At first, a player guesses random locations, but once they get a hit on one of the other player’s ships, they begin to search more closely around that area. Figure 1 describes this process in more detail, but essentially the algorithm first puts random parameters into binary star simulations to see which ones end with the desired event, and then tests parameters near the successful ones.

Figure 1: An illustration of the STROOPWAFEL algorithm. In the first stage random binaries are simulated to see if they result in an event of interest. Then in the next stage, distributions are drawn around the parameters that found successful events. Parameters in the distribution are then tested in the final stage. In the top panels of the left and right squares there are many more hits after the distribution is no longer randomized. (Fig. 1 in the paper)
The algorithm was incredibly successful. It was able to find 25 to 200 times the amount of mergers than other methods, improving simulation speeds by factors of 100. Figure 2 shows this pictorially. Initially, the rates of successful events per simulated binary is the same as traditional methods, but once they begin searching around the parameter spaces found in the exploratory phase, the number of hits increases by quite a bit.

Figure 2: The y-axis is the number of binary systems that end in the desired event. The x-axis is the number of systems simulated. The gray dashed line is the traditional random sampling result. As the number of successful events increases, the uncertainty in population statistics decreases. BH=Black Hole, NS= Neutron Star
These are promising first results from an algorithm named after a Dutch cookie. By speeding up computation times, astronomers will be able to further refine their theories and make new discoveries about the origin of these mysterious events. After implementing this algorithm, it will be feasible to introduce more initial parameters and explore variations on the assumed model. The authors plan to make future improvements to the model and it has applications to other computational fields.