Title: The cosmology of sub-MeV dark matter freeze-in
Authors: Cora Dvorkin, Tongyan Lin, and Katelin Schutz
First Author’s Institution: Department of Physics, Harvard University, Cambridge, MA, USA
Status: Pre-print on arXiv
Dark matter—what is it good for? As it turns out, quite a few things: assuming our understanding of gravity is correct, it can explain why galaxies form the way they do, why they move how they do, and why our universe is as old as it is. But what is dark matter? In today’s paper, the authors explore one potential answer to that question.
How does dark matter “freeze in”?
The dark matter candidate in today’s paper has two characteristics—how it’s produced and the sub-MeV mass of the particle—both of which are specified by the temperature of the universe. In the early universe, everything was hot enough that Standard Model (SM) particles could collide or decay with enough energy to produce dark matter (DM) particles, which are not predicted by the Standard Model. This could go on until the universe cooled enough that the process became energetically impossible, and the total number of dark matter particles became constant, or froze in. Exactly when the process stops depends on the mass of the particle, which sets the effective temperature of the particle that we can compare with the temperature of the universe.
Freeze-in is a great mechanism for dark matter production because how much dark matter is produced is independent of the initial conditions on the universe, making it pretty general. However, it also comes with a tiny coupling constant (which controls how strongly it interacts to SM particles), making it difficult to find with terrestrial accelerator searches. On the other hand, using astronomical probes could be much more promising for placing mass constraints on the DM particle!
Astronomical probes meet thermal histories
The key to testing freeze-in dark matter with astronomical observations lies in the velocity distribution of the particles. This is important because the particle’s cross section (which we can think about as strength of interaction with other stuff) scales as v-4, keenly depending on the details of the distribution. The distribution itself depends on the thermal history of the particles: the freeze-in dark matter, when created, is nonthermal, meaning that most of the particles have low velocities from just popping into existence and merrily carrying on (see the blue line of the inset of Figure 1). It’s possible that the dark matter velocity distribution has stayed mostly the same from its creation until today, or the interaction of the dark matter particles with each other could have thermalized them (see the red line of the inset of Figure 1). In the latter case, the particles would have interacted enough for all of them to be at the same temperature, which would turn its phase space into a Maxwell-Boltzman distribution, thus raising the average speed of the particles. In today’s paper, the authors consider both cases to put mass bounds on the particles.
In either case, the high-velocity nonthermal beginnings of the dark matter prohibit clustering of dark matter on small scales. The particles could be moving too fast on small astronomical scales (say, at the centers of galaxies) to form very intricate and stable structures. The authors consider how this would affect several observations, including the Lyman-α forest, strong gravitational lensing of quasars, stellar streams, and Milky Way satellites analyzed by the Dark Energy Survey (DES) collaboration, and plot the corresponding mass limits in Figure 1. They also predict how the Hydrogen Epoch of Reionization Array (HERA) and Vera Rubin Observatory will provide even better constraints on their dark matter candidate’s mass in the future. For the sake of keeping this summary brief, we’ll leave off the summary of each of these probes, providing instead a different astrobite or link to give readers a taste of why these probes are important. However, we will explore another bound the authors put on the mass: that of dark matter-baryon drag!
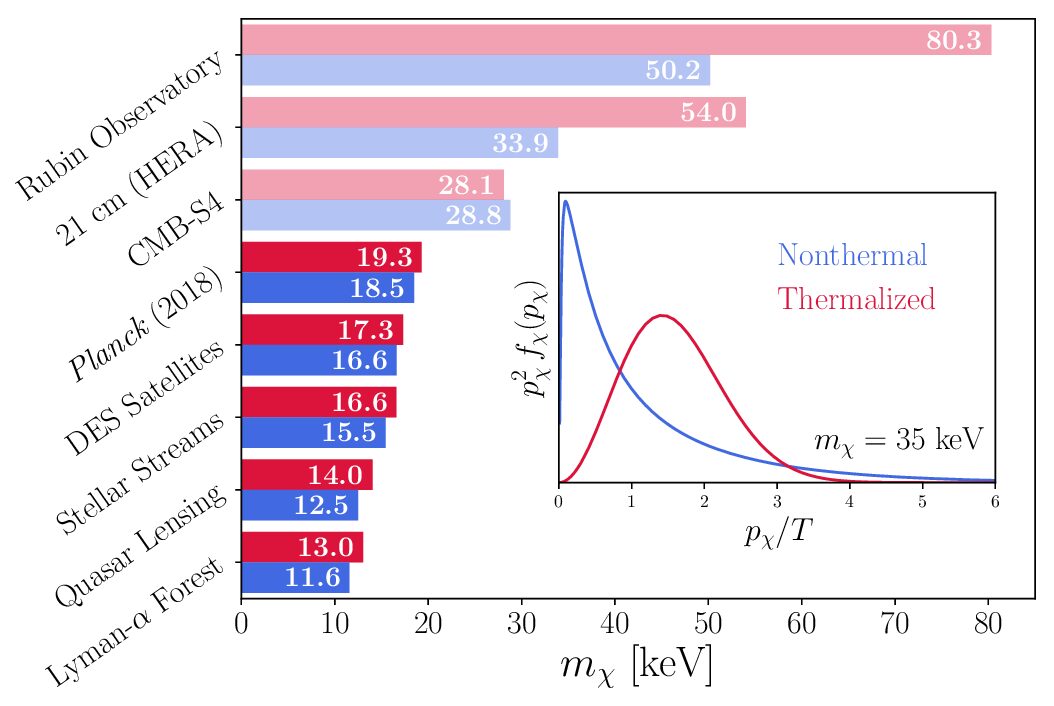
Figure 1: The figure shows mass bounds on freeze-in dark. Dark shaded bars correspond to already excluded particle masses, while light ones correspond to projected future measurements. The colors are different depending on whether the dark matter phase space remains nonthermal (blue) or thermalizes through self-interactions of the dark matter (red). In the inset, the authors show the phase space of dark matter if it remains nonthermal (blue) and if it themalizes through self-interactions (red). Figure 1 in the paper.
Dark matter is a drag
The interaction which allows dark matter to be produced from SM particles in the early universe doesn’t go away as the temperature of the universe drops and new dark matter particles are no longer being produced. This means that the SM and DM particles are not just attracted by gravity, but also to a lesser extent by this same interaction. One way to visualize this is like taking a bag full of heavy magnets out of a car: it’s hard not just because of the mass of the bag, but also because they’re being attracted to the car magnetically. This additional attraction between dark matter and SM particles (also known as baryons) causes a dark matter-baryon drag. Unlike the small-scale clustering, this effect depends on the low-velocity part of the dark matter’s velocity distribution. This effect is strongest before and during recombination, and is thus best seen in the Cosmic Microwave Background.
The drag force enhances the first peak in the CMB, while higher-order fluctuations in the power spectra are suppressed. When considering freeze-in dark matter, the high-velocity dark matter phase space leads to a smaller drag rate compared to dark matter with cold initial conditions which is popular in the literature, and thus smaller “wiggles” in the power spectra (see Figure 2). This allows the authors to put constraints on the particle’s mass by comparing with the Planck 2018 results, and predicting constraints by future CMB experiments like CMB-S4 (final two constraints in Figure 1).
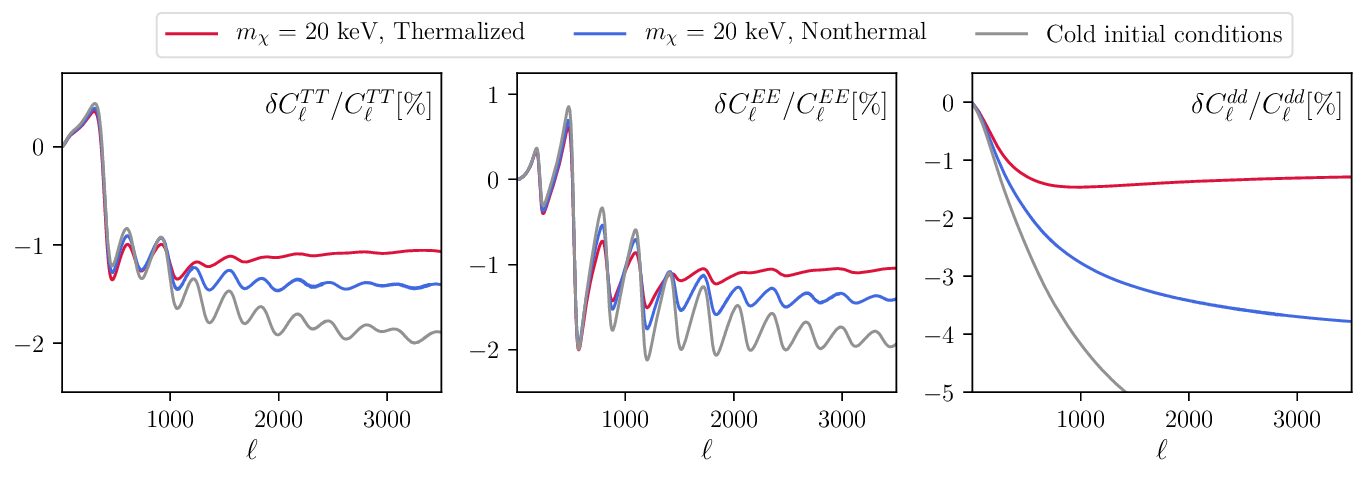
Figure 2: Effect of dark matter-baryon drag on CMB temperature, polarization, and lensing power spectra. The authors show the cases of freeze-in DM with mass of 20 keV for different DM thermal histories in red and blue. They also show the effect for dark matter with the same cross section and cold initial conditions, as a comparison with different production mechanisms. Figure 2 in the paper.
Conclusion
With the suppressed small-scale clustering and baryon-dark matter drag, the authors have been able to exclude freeze-in dark matter masses below ∼19 keV, leaving the 20-1000 keV range to explore. Not only that, but they have shown how instruments which will be coming online in the next few years will be able to test freeze-in masses up to almost 100 keV, further narrowing the available mass range. This will not only complement earth-bound accelerator tests of such dark matter candidates, but also allow us to carve deeper into the enormous range of potential dark matter masses—bringing us one step closer to the light.
Astrobite edited by: Wei Vivyan Yan
Featured image credit: A. S. Borlaff et al.