Title: Non-perturbative halo clustering from cosmological density peaks
Authors: Tobias Baldauf, Sandrine Codis, Vincent Desjacques, Christophe Pichon
First Author’s Institution: Department of Applied Mathematics and Theoretical Physics, University of Cambridge, CB3 0WA, Cambridge, UK
Status: Preprint on arXiv
Do you ever just want to be a kid again? Do you look around at the complications of adult life and wish for a time when things were just a little simpler? For better or worse, you can’t – but a quest for a simpler time can be useful in studying the complicated world of dark matter halos!
Today, cosmologists infer cosmological parameters by looking at the spatial distribution and clustering of galaxies. Galaxies live in dark matter halos – so it is important to understand how halos are distributed in space before we can fully understand the galaxy distribution. However, the halo distribution is quite complicated – aside from living in the cosmic web produced by nonlinear structure formation, as discrete objects, halos carry their own conceptual baggage that needs to be unpacked. To study how halos cluster in space, it can help to return to their childhood, when the halos were simpler and less molded by the world around them. Today’s paper is chock-full of great results – but today we will focus on a few in particular that help us with this past exploration of halos. Namely, how early-time cosmological maxima (peaks) in matter density can help us describe the spatial distribution of halos today!
Dark matter halos – an exclusive club
One way to describe the modern-day halo distribution is through the aptly-named halo model. The halo model has been wildly successful given the simplicity of its assumptions – and has seen wide use in modern cosmology. The halo model makes the following assumptions: 1. all dark matter lives in halos, and 2. halos don’t overlap. The ingredients of the halo model are then the halo mass function, the halo profile, and the halo bias (we won’t go into detail here but check out the linked bites!). It is usually further assumed that halos are spherical (in reality, they are not), which is a good approximation on average. From the second assumption of the halo model we come naturally to the concept of halo exclusion. Since halos are not allowed to overlap, we can imagine them as hard spheres that don’t pass through each other. This means that no two halos can ever get closer than the sum of their radii!
Whipping up some cosmological peaks
A natural question is then: is this exclusion just the result of our simple model for halos, or is it telling us something physical about the way halos form? The answer to this question lies in a careful study of the precursors to halos, which today’s authors provide. They look at young, not-yet-halos (aka “proto-halos”) that form at local density maxima of the (smoothed) early-time matter distribution. These maxima are called peaks (see Fig. 1). Peaks are often described by their “height” ν, which is proportional to their deviation from the mean density (density contrast δ, vertical axis in Fig. 1). In the peak framework, the locations of the peaks are assumed to be the sites of halo formation – and at early times define the center of protohalos. Peaks are discrete (like halos) rather than continuous (like matter), and you can roughly think of the process of halo formation as a protohalo collapsing to produce a halo (though its center of mass moves as this happens).
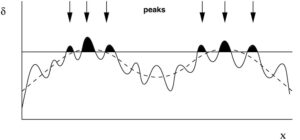
Figure 1: A cartoon of peaks in the spatial matter density distribution. δ is the density contrast (fractional difference from mean density). Peaks above a certain height are pointed out and shaded. Adapted from Peacock.
Now that we understand a little about where halos may come from – what does this have to do with exclusion? Well today’s authors (and in an earlier paper) emphasize that peaks obey exclusion – and this is before halos form, so exclusion is an important physical effect of the early-time universe! The authors provide an in-depth study of this phenomenon in numerical simulations – part of which explores exclusion in peak clustering and how those peaks match up to halos.
Taking a peak at some results
The authors provide predictions using the peak framework for the correlation function of peaks – essentially how likely two peaks are to be separated by a given distance r. The predictions incorporate the exclusion of peaks, which results in a characteristic drop in the correlation function ξ(r) for small r (Fig. 2). When 1 + ξ(r) = 0, the probability of finding two peaks separated by that distance is zero – and this is exactly the behavior expected of exclusion (as we discussed for hard spheres). The peak predictions are given by the red lines in Fig. 2 for two different assumptions – the first (dashed) assumes the peaks are of the same height (peak height very roughly corresponds to protohalo mass), while the second (solid) is for peaks of different heights. Notably, the exclusion feature only shows up for correlations between peaks of different heights! This last prediction matches up quite well with the black points – which are protohalos as measured in an N-body simulation. The authors identify these simulated protohalos by finding halos in the final-time output and tracing back their member particles to the initial conditions. Also shown is the simplest possible model for the clustering of peaks – that of linear bias – which is quite far from the simulated protohalos and the peak prediction.
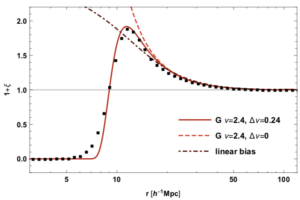
Figure 2: Clustering signal (correlation function) of traced-back proto-halos [black points] with several predictions, including: the simplest model of linear bias, the numerical prediction of today’s paper for peaks of the same height (Δν=0, dashed) and of different heights (solid). The exclusion transition to zero is clear for both the numerical model with exclusion and the simulated halos. Adapted from Fig. 3 of today’s paper.
Clearly exclusion is present in peak clustering at early times, but how does it affect their time-evolution into the modern-day halo distribution? The authors explore this by providing a simplified model for the time evolution of the peak predictions for protohalo clustering (Fig 3). Fig. 3 shows the same quantity as Fig 2 (1+ξ(r)), where points (excluding the stars) denote the traced-back (proto)halos and curves denote the evolved peak prediction. Here you can think of the time as being indexed by D+. At early times (near the initial conditions), there is near perfect agreement between the peak prediction and the simulated protohalos. But as time goes on and the halos lose their “proto”-ness, the exclusion feature grows and gets pushed to smaller scales, and the evolved peak prediction becomes less accurate (though it is still qualitatively similar).
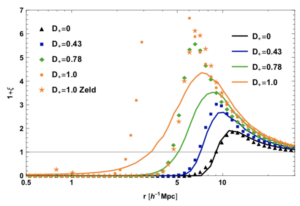
Figure 3: The correlation function (same as Fig. 1) at different times. D+=0 denotes the initial conditions (black), and D+=1 (orange) denotes the final time. Points denote the correlation of simulated halos, while lines denote the prediction of today’s paper (with time evolution). As time evolves, the exclusion feature grows and shifts to smaller length scales. Adapted from Fig. 8 of today’s paper.
Today’s paper shows that peaks can provide insight into the evolution of the halo, and, by extension, galaxy distribution. We saw how this was possible through the careful study of peaks and halos, specifically through the phenomenon of exclusion. In addition to providing a better understanding of halos, peaks can also improve Baryon Acoustic Oscillation reconstruction techniques. Furthermore, today’s authors hint that in some cases the exclusion feature for peaks and halos may actually be visible for certain observed galaxy samples. These improvements could help data analyses approach a level closer to peak performance in recovery of cosmological parameters!
Astrobite Edited by: Jamie Wilson
Featured image credit: Adapted from Peacock (IPAC)