Title: Cosmological gravity on all scales: simple equations, required conditions, and a framework for modified gravity and Cosmological gravity on all scales II: Model independent modified gravity N-body simulations
Authors paper I: Daniel B Thomas
Authors paper II: Sankarshana Srinivasan, Daniel B Thomas, Francesco Pace, Richard Battye
First author institution: Jodrell Bank Centre for Astrophysics, School of Natural Sciences, University of Manchester
Status: Phys. Rev. D (paper I) [Closed access], JCAP (paper II) [Open access]
Today’s bite features two related papers about how to test gravity on the largest scales in the universe, the first focusing on the theoretical framework and the second focusing on implementing this model in simulations. Daniel Thomas (first author on paper I) was interviewed on the Cosmology Talks YouTube channel about this work and you can watch the whole 45 minute discussion for more details on both of these papers.
Gravity. While it is the most directly familiar of the fundamental forces to most of us, it remains one of the most mysterious and difficult to test. In 1915, Albert Einstein put forth his General Theory of Relativity, based on the principle that space-time is a mutable fabric, one which mass-energy warps and bends according to the Einstein field equations. General relativity (GR) has seen enormous success in the 100 years since it was introduced. It has been on the length scales of the Solar System. It has made predictions about black holes. It predicted the existence of gravitational waves. All of these phenomena have agreed with the GR prediction stunningly, and been confirmed by experiment. As such a successful theory, it forms the mathematical backbone of the study of the universe as a whole: cosmology. However, the universe is much bigger than the Solar System, approximately 15 orders of magnitude larger, and testing gravity on these large length scales is difficult. Just as concepts from classical physics break down when you start looking at very small objects like atoms, it is possible that GR, while a very good theory on Solar System length scales, fails in certain ways on very large scales.
Here we bump into the first problem of exploring modifications to GR: there are virtually infinite ways for gravity to not be general relativity, so how do we go about trying to figure out what the right theory is? There are a couple of different broad approaches:
- Parametrisation. In areas where we expect gravity to be “weak”, e.g. not near black holes and not on very large scales, we know that gravity must reduce to Newtonian gravity. We can parametrise different measurable deviations from Newtonian behaviour by a set of parameters (e.g. different speeds of light). General relativity makes certain predictions for what each of these parameters are, and we can compare the measured parameters to the GR predictions and obtain constraints on deviations from GR.
- Specific models. If one can come up with a particular, different, theory of gravity (perhaps our universe is actually part of a larger 5 dimensional bulk, as in DGP gravity, or there are new, as yet undetected particles which change how gravity works, as in scalar-tensor theories) in principle you can make specific predictions about how observable quantities are different than in general relativity.
The advantage of specific models is that you can in principle look for very distinct signatures of that model and compare them to observations. The downside is making predictions about observables is often very difficult in specific models, and they can become arbitrarily complex very quickly. Further, if the true theory of gravity is one that you aren’t studying, then you will not be able to extract any information about the correct theory. In contrast, some sort of parametrised approach, or model independent approach is generally sensitive to a much broader class of theories, which makes it a better tool for general searches for what might be going wrong with GR. The downside with parametrised approaches is that they only work in certain circumstances, often when gravity is weak. These circumstances are often also the regions where we don’t expect GR to fail, so extracting data from them can be very difficult. Additionally, parametrisation doesn’t give you physical information about what’s causing the deviations. Several different models could all have similar predictions in the weak field regime, so it may be impossible to track down what source causes the effect.
The authors of these papers propose a framework that can be used to make cosmological simulations which are compatible with a very large class of modified gravity theories, similar to the parametrised approach taken around Newtonian mechanics. However, to make the mathematics accommodate all cosmological scales, the standard post-Newtonian parametrisation cannot be used, since that only holds for weak gravity and small scales. Paper I sets up the mathematics needed instead, and lays out conditions for which theories of gravity will be accommodated by this framework instead of choosing specific ones.
Scales and tools in cosmology
The standard model of cosmology, Lambda-CDM, is based on general relativity and has made extremely precise predictions, provided that in addition to ordinary matter we include cold dark matter (the CDM) and a cosmological constant driving accelerated expansion (the Lambda). While dark matter was originally postulated to explain the rotation curves of galaxies, the evidence for dark matter is now much stronger and further reaching. While it might be possible to completely do away with dark matter by changing the theory of gravity, it is extremely difficult to do so, and most studies of modified gravity assume that dark matter is present and change the theory of gravity. Lambda-CDM does still have certain problems which provide tantalising hints to where our theory might be breaking down, modified gravity might be a way of solving some of these problems.
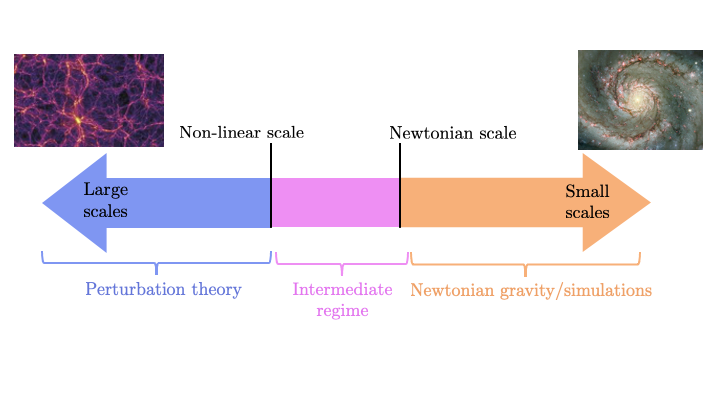
There are two well understood regimes in cosmology, on either end of the length scale. On small scales, we can use Newtonian physics, just like we do on Earth, as the curvature in the gravitational potential isn’t too large. While this is tricky because Newtonian gravity involves non-linear equations of motion, we have developed techniques for making predictions in certain cases, and where we can’t solve things exactly we can run simulations on supercomputers.
On very large length scales we rely on mathematics called cosmic perturbation theory. The starting point is to assume the universe is perfectly homogeneous and isotropic, which leads to the exact solution: the Friedmann equations. From there, we consider perturbing the universe slightly from this exact solution, which we do by introducing two potentials Φ and Ψ. Doing this leads to a set of coupled linear equations, which we can solve by ignoring higher order terms like Φ2 and Ψ2.
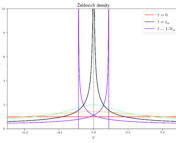
Perturbation theory breaks down at the “non-linear scale” where densities become large, whereas Newtonian theory breaks down above a certain length scale where velocities become large and relativity becomes important. In principle, these two scales are different as shown in Figure 1, but for Lambda-CDM, they happen at about the same time (~10 Mpc). This is good news if Lambda-CDM is the right theory as on large “linear” scales, we can use perturbation theory to make predictions, and on small scales we can use the results of Newtonian techniques and simulations to make predictions. However, in modified gravity, there is potentially an “intermediate regime” where neither of the tools in the cosmologist toolkit work. That’s where today’s papers come in.
The mathematical framework
The first paper sets up a mathematical framework to connect the regimes where we have tools that work, extending through the intermediate regime. The equations are rather long and nasty, but the basic gist is the following: in both the Newtonian limit and linear perturbation theory there are two equations about the gravitational potentials, one which states how much they differ (in GR they are equal) and one which relates the potential to the matter density called the Poisson equation (second spatial derivatives of the potential are proportional to the matter density). Because both regimes have Poisson equations, it is tempting to say something along the lines of “the potential arising in cosmic perturbation theory is basically the same as the Newtonian potential.” This paper makes this rough idea of a correspondence more precise, by developing a set of potentials which work on all cosmic scales—large linear scales, the intermediate regime, and the small Newtonian scales—deriving equations relating this potential to the matter density. For the mathematically minded, this is Equation 3.4 in paper I. The main point is that if there is no intermediate regime, then some of these terms disappear. That means we have something looking like a Poisson equation again, but this time crucially, it applies continuously on both large and small scales!
Roughly speaking, this framework can therefore be used on any theory of gravity which does not have an intermediate regime. While this might sound restrictive, it is significantly broader than the method of choosing individual theories, and it does actually include some specific theories people care about, for example Hu-Sawicki f(R) gravity. A whole algorithm for determining if a particular theory is appropriate for this framework is included in Section V of the paper.
Simulations
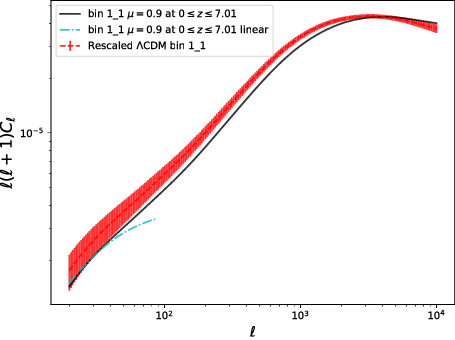
Armed with tools which work on all scales for a wide group of theories of gravity, paper II sets up running modified gravity simulations according to the mathematical framework set up in paper I. The simulations which are run are rather simplistic, only allowing the Poisson equation to vary from GR in time, rather than allowing a more general variation in both time and space, but this is done as a proof of concept to demonstrate how much more information can be extracted. One point that demonstrates the importance of such simulations is shown in Figure 2. Without a way to gain information about modified gravity in the non-linear regime (which is what we get from simulations) we could only use data from the largest scales to extract information. Figure 2 shows the sort of data we could expect from upcoming surveys like the Euclid satellite. The fact that the blue line (linear perturbation theory) is only an accurate prediction for a small fraction of the data means that a huge amount of potential data simply can’t be analysed if we don’t extend the cosmologists’ toolkit.
While these papers are not the first to demonstrate how important the non-linear regime is for gathering information from future surveys, they do make an important step in laying out tools which will be useful in making predictions and analysing data. Certainly there are other complicated factors to account for on small scales, particularly the role of baryonic matter, but future work building on this pushes the boundaries of where we can test gravity in cosmology.
Edited by: Ciara Johnson
Featured image: Alex Gough. Image of cosmology simulation from TNG simulation.