Title: Gravitational instability: an approximate theory for large density perturbations.
Author: Y. B. Zel’Dovich
Author’s institution: Institute of Applied Mathematics, Moscow
Status: Published in Astronomy&Astrophysics, available via ADS
The early universe was nearly exactly the same everywhere, with deviations from the mean density being only about ten parts per million. Today, we see networks of stars, galaxies, and clusters, all tracing an intricate and invisible skeleton of dark matter. How do these small perturbations in the early universe grow to the large, rich, structures we see on all scales today?
Today’s classic paper provided one of the key insights and approximations that is still widely in use today. The secret is the prediction of cosmic pancakes. Yes really! Though the term “pancake” isn’t used in the original 1970 paper, by 1972, this paper describes the result as “during the stage of large perturbations, the theory predicts the formation of plane contractions (‘pancakes’)”. To this day, the term “Zeldovich pancakes” is still used when describing this approximation of structure formation.
How pancakes are born
For this paper, Zeldovich considers the evolution of a pressureless and collisionless form of matter. This approximation applies both to normal matter and dark matter on large scales, but doesn’t work for normal matter on small scales (you and I are proof that normal matter has internal forces and pressures!). From a modern perspective, the approximations laid out here are used on cold dark matter which is favoured by today’s standard cosmological model.
This paper considers how particles move from their initial to their final positions under the influence of both the expansion and gravitational attraction. The simplest approximate solution one could think up to this problem is to consider all particles just drift with an initial velocity set up by the gravitational potential set up at the initial time. This approximation, where particles follow simple trajectories based on the initial distribution of matter, is called the Zeldovich approximation. This approximation is known to work well on large scales where deviations from the mean density are small and structures have not yet formed.
What this paper does for the first time is extend this approximation into the “non-linear regime” where the densities can be very different from the background density. The result of this is that an ellipsoid cloud of pressureless matter will collapse along one of its axes first and flatten into a pancake.
What is perhaps concerning about this approximation is that at the point where the cloud is fully collapsed, the matter density becomes infinite (since a 2 dimensional pancake has no 3 dimensional volume). This moment, when particles from different initial positions “stack up” at the same final point is called “shell crossing”. Shell crossing presents a problem in the mathematics which is still challenging to go beyond even 50 years later.
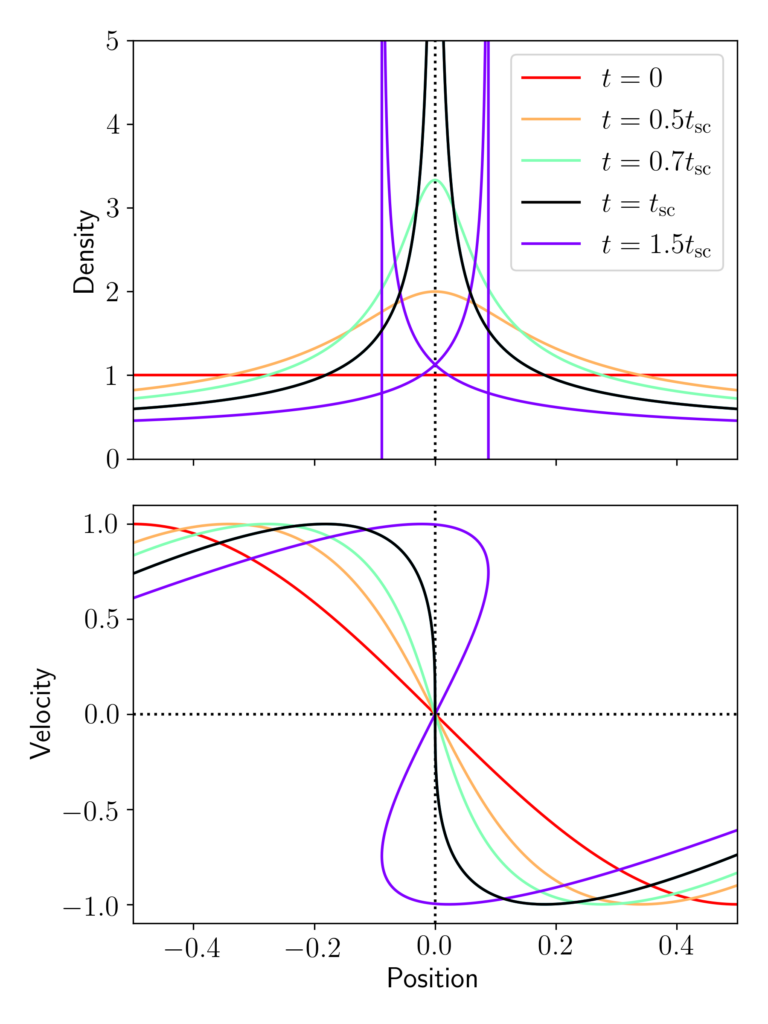
To see why, consider the 1 dimensional version of this problem, with just a single line of particles, moving with some initial velocity (this is shown in Figure 1). At the start, everything is well behaved, and particles just move towards one another, with their final positions being in one-to-one correspondence with their initial positions. After a long enough time, particles which started on the left will meet particles which started on the right, and the two streams of matter will begin to overlap. The first instance where two particles which started from different initial positions end up at the same final position is called “shell-crossing”. Since we’re considering matter which doesn’t interact with itself, the stream from the left and from the right continue to flow through each other, creating a region in the centre where there are 3 particles at the same position moving with different velocities. You can see this in the bottom panel of Figure 1 on the t=1.5tsc line. There is a region of final positions between -0.1 and 0.1 where there are 3 velocities for each position. Looking at the corresponding density in the upper panel of Figure 1, we can see that this “muli-stream” region is separated from the well behaved “single stream” region by walls of infinite matter density.
This business of multiple streams is tricky mathematically, as we cannot continue to model the matter as a single simple fluid, as fluid mechanics requires that variables like the velocity are single valued everywhere. Understanding how to push the modelling of gravitational collapse into this multi-stream region continues to be an active area of research.
Zeldovich didn’t take this idea of particles flowing through each other seriously though, instead stating that particles should instead “abruptly come to a standstill by encounter with the disc [pancake]…this produces a receding shock-wave”. This abrupt halt would cause any ordinary matter following along in the collapse to create immense pressures and heat up, creating circumstances where stars can form. Additionally these shocks would tear the large collapse structure into smaller fragments, leading to a “top-down” picture of structure formation. This is in contrast to the “bottom-up” or “hierarchical” picture of structure formation, where small dwarf galaxies form first, then later merge to form larger galaxies and clusters.
The state of pancakes today
This top-down approach is no longer the preferred method for galaxy formation; the cold dark matter in the standard cosmological model predicts a bottom-up approach. However, the observation of the large scale structure of the universe seems to indicate that the truth is somewhere in between these two methods, with structures forming on all scales. However, the Zeldovich approximation, and the existence of cosmic pancakes, does still play an important role in modern cosmology.
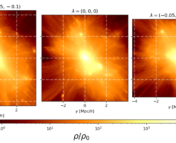
This hybridised model between the top-down and bottom-up approaches is called the “cosmic web”. The dark matter, which outnumbers ordinary matter 4-to-1, collapses first to form pancakes, then along another axis to form one dimensional “filaments”, and then further to form “knots”. This network of sheets, filaments, and knots, formally of infinite density, form a skeleton for the universe, one which the ordinary matter roughly traces.
Another important role for the Zeldovich approximation is in cosmological simulations. In modern language, the Zeldovich approximation is a significant part of a more complete method called Lagrangian perturbation theory (LPT). Cosmological simulations are an important part of learning about the late time universe, as the physics involved is very complicated to track analytically. However, simulations are also computationally expensive and take a long time to run. We know from the cosmic microwave background what the matter density looks like at redshift z=1100 (when the universe was ~380,000 years old). To avoid having to run the simulation over the entire evolution of the universe, we can take advantage of the fact that at early times structures have not yet had time to fully collapse, so we can work with the physics directly. That’s where LPT comes in. Instead of starting their initial conditions at z=1100, they usually use LPT to analytically evolve the CMB initial conditions to somewhere between z=50 and z=100 (when the universe is 15-50 million years old). From there the simulation can actually run on all the particles, keeping track of the complicated physics for us.
While the Zeldovich approximation is a simplistic way of looking at how structures form in the universe, it provides some excellent insight into the dynamics of collisionless dark matter, and sets the groundwork for a numerical tool still used in state of the art simulations. I guess for the universe a breakfast of pancakes really is the most important meal of the day!
Astrobite edited by H Perry Hatchfield
Featured image credit: Alex Gough