Title: A More Informative Map: Inverting Thermal Orbital Phase and Eclipse Lightcurves of Exoplanets
Authors: Emily Rauscher, Veenu Suri, Nicolas B. Cowan
First Author’s Institution: University of Michigan, Ann Arbor
Status: Submitted to AAS Journals, open access
During a recent visit to the Dutch National Maritime Museum I came across the world map from 1648 AD by cartographer John Blaeu. In addition to being the first world map of the Earth that adhered to the Copernican worldview, Blaeu’s map is an extremely detailed document of the knowledge of the world at the time sourced solely from the information gathered by explorers from their travels through ages to the far reaches of the world. It’s inaccuracies and subjectivity to the western view of the world are quite amusing, but there is still a level of high detail and surprising accuracy. Through these details, it is clear that cartographers must meticulously piece together information from a large number of sources of varying reliability. Creating maps of exoplanets, also beginning to be known as Exocartography, is an equally challenging observational and mathematical problem which is addressed by today’s paper.
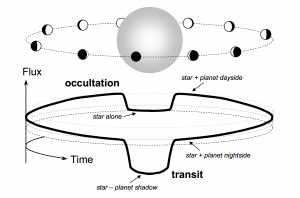
Figure 1: Schematic of transits and occultations (also referred to as secondary eclipse) in an exoplanetary system. (Figure 1 in Winn (2010))
Creating maps of exoplanets can give an idea of the presence of climatic features in the planetary atmosphere or surface which when compared to predictions from general circulations models can give us an insight into physical processes in play in their atmospheres. Observations in this context comprise of continuous monitoring of the brightness of a planetary system as different regions of the planet come into view. A schematic of these occultations is shown in Figure 1. Disk integrated flux (total flux from the planet’s surface which is visible as a circular disk) of the planet observed as a function of time in this way can then be converted to flux (more easily so for a tidally locked planet) as a function of spatial locations on the planet (which are coming into view as a function of time) to render a 2D brightness map of the planet for the chosen wavelength band.
However, this technique can be sensitive to the choice of map structure and uncertainties in the orbital parameters of the system and hence has only been reliably attempted for a few well-studied hot Jupiters(for example HD189733 and hot super-Earths to date. Today’s paper proposes a method that maximizes the information in the flux maps retrieved from phase curves and secondary eclipse observations while accounting for the effect of orbital parameter uncertainties.
A closer look at exocartography
It may still be a few decades before we successfully send a spacecraft to the get an up-close image of the nearest exoplanet. Till then, astronomers will mostly be busy extracting brightness maps of exoplanets from their high-precision photometric observations. Only phase curve (i.e. not including the secondary eclipse) observations in this context are more sensitive to the longitudinal distribution of brightness, while most latitudinal information comes from the secondary eclipse. Considering the wavelength band in which these observations are taken, infrared phase curves like those obtained using Spitzer are more sensitive to the thermal emission from the planet, while shorter (optical) wavelengths usually probe the reflected light, which can be used to get an albedo map of the planet.
Once you have the phase-resolved or eclipse observations for a particular wavelength band, the first step in converting them to spatial flux maps of the planet conventionally involves assuming a 2D brightness map structure and fitting the observations with a disk-integrated flux curve model (a function of the orbital phase) which has a one to one correspondence with the chosen map. But for a planet which could, in fact, have a very general distribution of spatial brightness, what’s the functional form for the 2D map should you choose to start with?
The best mathematical way for representing a signal with a general functional form is actually to decompose it into a linear combination of Fourier basis functions or basis maps in this context. The reason this is the best choice is the orthogonality of Fourier basis functions which makes them informatically independent of each other and prevents any scrambling of information when using a linear combination of them to represent a signal. In case of brightness maps, which are essentially functions defined on the surface of a sphere, spherical harmonics play the role of orthogonal basis functions and hence are a good choice to represent the map structure for the planet’s brightness. This is where lies the key problem addressed by today’s paper — light curves corresponding to a set of orthogonal basis maps (like spherical harmonics) may not be orthogonal themselves, especially in the case of eclipse-only observations!
Orthogonalize!
Authors of today’s paper propose to use a principal component analysis (PCA) approach to orthogonalize the light curves (corresponding to spherical harmonics maps for a chosen orbital realization) to get a set of eigen-lightcurves (or eigencurves), which can then be used to construct flux curve models to fit the thermal phase curve, eclipse or combined observations. Finding eigencurves in this context means getting the eigenvectors of a matrix composed of the initial set of light curves as column vectors, which is done by a simple linear transform of these light curves using the coefficients obtained from PCA. PCA essentially tries to determine the axes of variance and covariance in the input matrix of initial light curves. These axes, in the context of constructing the flux curve model, are like independent lines of forces along which a linear combination of eigencurves acts to give the final model for the signal. Determining the eigencurves means determining these independent lines of forces.
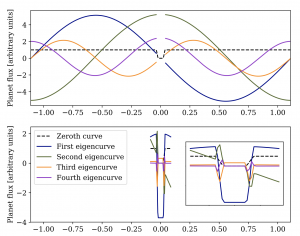
Figure 2: Time-varying eigencurves (horizontal axis showing time from the center of secondary eclipse in days). The first panel shows the case for full orbit without secondary eclipse and the second panel shows only eclipse case. Figure 2 in the paper.
The eigenvalues for each eigencurve intuitively represent the relative amount of information contributed by an eigencurve to the total light curve signal, and hence they can be ranked and chosen according to their information content. Eigenmaps can be determined by a linear combination of the initial set of maps using the same PCA coefficients as obtained for corresponding eigencurves. A linear combination of eigencurves (with linear coefficients free to be constrained by observations) finally forms the flux curve model which is fit to the observations. The authors perform this exercise for three cases: simulated observations for full orbit phase curve (without secondary eclipse), only secondary eclipse (with a fraction of before and after orbit), and real observations of the hot-Jupiter HD189733 with both phase curve and eclipse combined. The eigencurves and the corresponding eigenmaps used by them for retrieving the brightness maps for the first two cases are shown in Figure 2 and 3.
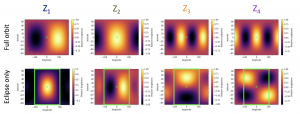
Figure 3: Spatially varying 2D eigenmaps for the two cases shown in Figure 2. ‘X’ in the bottom figure is the point permanently facing the star (assuming the planet to be tidally locked), and the green box in case of eclipse only observation marks the range of longitudes probed by the observations. Figure 3 in the paper.
Comparing the eigencurves with their corresponding eigenmaps (Figure 2 and Figure 3), it is evident that each eigencurve for the full orbit without eclipse case encodes paired pieces of spatial information along the longitudes of the planet, while most latitudinal information comes from the eclipse (second eigenmap (Z2) onwards in Figure 3). The PCA approach ensures that the eigencurves used to construct the model flux curve are orthogonal even for the eclipse only case. The authors use the eigencurves for combined phase curve and eclipse observations of HD189733 by Spitzer in 8 μm channel and retrieve the longitude of the dayside hotspot (region of peak temperature on the planetary hemisphere facing the star) and the flux contrast of the hotspot, which are both consistent with the results obtained from previous studies. Additionally, the authors also investigate the effect of orbital parameter uncertainties by checking the sensitivity of PCA coefficients to construct eigencurves from original light curves for orbital realizations within one-sigma uncertainties.
Usually, correlated noise in the detectors used for high-precision photometric observations are corrected for together with the fit for astrophysical parameters, which can lead to correlations creeping even in between the orthogonal light curves obtained from the PCA approach. This only calls for more caution when working with the high-quality mapping data which will be obtained from the James Webb Space Telescope. With the planned high-precision photometric observations in multiple spectral bands by JWST, we can look forward to combining the horizontal 2D mapping as discussed in today’s paper with information about the vertical atmospheric structure and get more reliable three-dimensional maps of exoplanets in near future.