Title: Early-Universe-Physics Independent and Uncalibrated Cosmic Standards: Constraint on Ωm and Implications for the Hubble Tension
Authors: Weikang Lin, Xingang Chen, and Katherine J. Mack
First Authors Institution: Tsung-Dao Lee Institute, Shanghai Jiao Tong University, China and Department of Physics, North Carolina State University, Raleigh, USA
Status: Available on arXiv
The arguably largest issue in cosmology (and a frequent topic of astrobites, for example, here, here or here) is the Hubble tension. This issue concern s agreement about the rate at which the Universe expands today, described by the Hubble parameter H0. We know that H0 is somewhere around 70 km/s/Mpc, meaning that a galaxy 1 Mpc away is pulled from us with 70 km/s due to the Universe’s expansion. However, we do not know the precise value of H0. Even worse, measurements of H0 with different observational techniques give conflicting values. For example, the analysis of the Planck satellite of the Cosmic Microwave Background (CMB), the remnant radiation from when the Universe was “just” 380 000 years old, suggest the relatively low value of H0=67.4+-0.5 km/s/Mpc. Measurements of supernovae’ distances, calibrated with Cepheids, in our local Universe, though, find the much higher H0=74.03+-1.42 km/s/Mpc. This discrepancy could mean that our current model of the Universe is wrong and needs to be changed.
One way cosmologists try to solve this problem is with new models for the early Universe before the CMB was emitted. Some examples include an additional dark energy component, more types of neutrinos, or interaction of neutrinos and dark matter. These “new physics” would impact the assumptions about the early Universe made in the Planck analysis and increase the H0 inferred from the CMB. However, the authors of today’s paper show that these efforts to solve the Hubble tension might be fruitless. They consider cosmological probes independent of the early Universe and find that the Hubble tension persists. Their idea? Use two unique scales – the sound horizons.
A tale of two horizons – rd and r*
The authors consider two important scales, the drag sound horizon rd and the recombination sound horizon r*. To understand these scales, we need to remember what the Universe looked like before the CMB was emitted. In contrast to the mostly empty and cold Universe today, back then, it was filled with a hot fluid of protons, free electrons, and photons. Photons continually scattered off the free electrons and their pressure kept the fluid from collapsing due to its gravity. Like any fluid, this particle soup also carried sound waves. Like in air, the fluid at some positions and stretched it out at others. The waves are related to the sound horizon, which at each time t is the furthest distance a sound wave could have travelled in some time t since the Big Bang. Both rd and r* are such sound horizons, although at slightly different times.
For r*, the relevant time is the time the CMB was emitted. This occurred once electrons and protons combined so photons no longer scattered off electrons and could travel freely. These “released” photons make up the CMB we observe today.
For rd, the relevant time is the end of the so-called “drag epoch”. During this epoch, the photon pressure prevented the gravitational collapse of the baryonic matter (i.e. protons and electrons). Once the photons were released, the pressure decreased until it was low enough that baryons attract each other gravitationally. The drag epoch ended shortly after the CMB was released, so rd is slightly larger than r*.
The values of r* and rd depend on the physics before the CMB was emitted. However, the difference between the two does not. It only depends on how the Universe expanded between the CMB release and the end of the drag epoch. This expansion in turn depends on the density of matter, which cosmologists measure with Ωm. Therefore, rd and r* together can measure Ωm without assumptions on the early Universe physics. Today’s paper combines this measurement of Ωm with other independent probes to estimate the Hubble parameter H0. But, how can we measure r* and rd?
Combining the CMB, Baryon-Acoustic Oscillations and Supernovae – without calibration
To find r*, rd and through them the matter density, today’s authors use three probes: Baryon-Acoustic Oscillations (BAOs), the CMB, and Supernovae Type Ia, without calibration. They call this combination Early-Universe-Model Independent and Uncalibrated Cosmic Standards (abbreviated by UCS).
BAOs are features of the galaxy distribution originating from the sound waves in the hot particle soup at the beginning of the Universe, which compressed parts of the fluids. These slightly denser parts attracted other matter via gravity, so they grew more and more prominent and are today visible as areas with more matter, more gas, and more galaxies. The distance between those overdense areas is related to the sound horizon rd at the end of the drag epoch. So, just by measuring where there are particularly many galaxies, we can infer rd.
The CMB estimates r* through its power spectrum (see this bite on using this power spectrum to measure the cosmological parameters). This power spectrum describes the temperature fluctuations in the CMB at different scales. Similarly to BAOs, these fluctuations are related to the sound waves in the initial particle soup. They are strongest at scales proportional to r*, which leads to peaks in the CMB power spectrum at these scales.
Combining the rd from BAOs and the r* from the CMB gives an estimate of Ωm. To refine this estimate, the authors further combined this result with measurements from Supernovae Type Ia.
Supernovae Type Ia are explosions of white dwarfs that have recently accreted matter. The mechanisms leading to this explosion are reasonably well understood, so we can use them as distance indicators (explained in this bite). Usually, supernova measurements are calibrated with other observables such as Cepheids. These calibrations tell us the supernovae’s absolute magnitude or intrinsic brightness, so it is easier to infer their distance. However, today’s authors try to rely on as few assumptions as possible, so they do not use calibration and instead keep the absolute magnitude of supernovae as a free parameter.
Using these methods, the authors arrive at a slightly different matter density, depending on which data sets they use (Fig. 1). However, all results agree with each other. Combining all UCS leads to Ωm=0.302+-0.008, which agrees with the original analysis of the CMB.
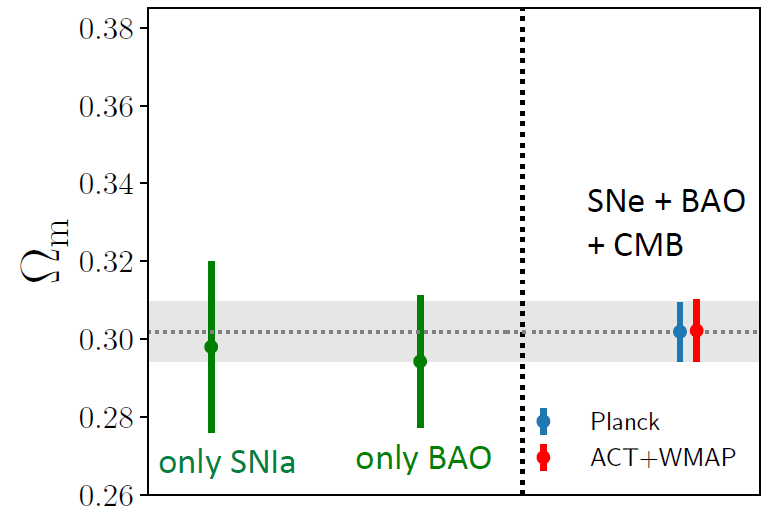
Figure 1: Matter density measured with the UCS method, either using only supernovae Type Ia (green, left), only the BAOs (green, right), or combining all three data sets. All values for Ωm are consistent with each other, which suggests that the combination is valid. Two different kinds of CMB data were taken, either those measured with the Planck satellite (blue) or with the (red). Adapted from Fig. 3 in the paper.
From the matter density to the Hubble parameter
So, what about the Hubble parameter? To find H0, the authors combine the measurement of Ωm with three other probes that are also independent of early Universe physics: Cosmic Chronometers (see this bite), the density of gamma-rays, and the cosmic large-scale structure, as measured by weak gravitational lensing. All of them are cosmological probes in their own right. Their precision for H0, though, is much lower than for the CMB or supernovae calibrated with Cepheids. However, with the Ωm measured from the UCS, the precision increases.
Figure 2 shows the results for H0 when combining the other probes with UCS, for supernovae calibrated with Cepheids, and for the Planck analysis of the CMB. The results from UCS, which are independent of early Universe physics, agree with the Planck values but are slightly in tension with the Cepheid measurements. Consequently, the discrepancy between the H0 from supernovae and cepheids and the Planck H0 cannot be due to the assumptions on the early Universe made in the Planck analysis. Changing the early Universe does not solve the Hubble tension.
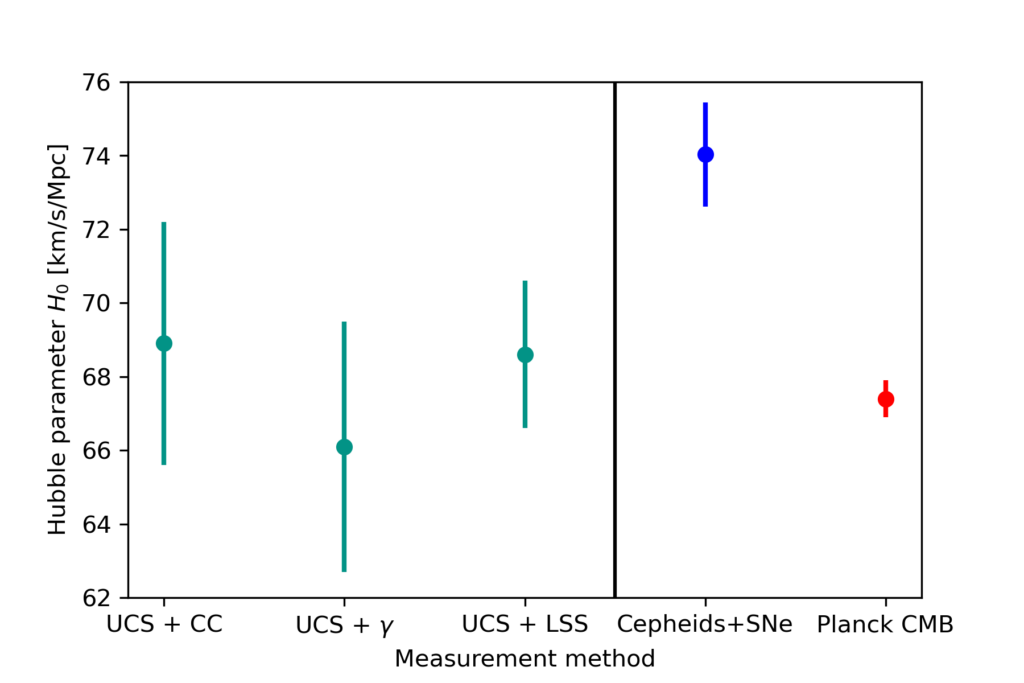
Figure 2: Hubble parameters measured with the UCS method described in the paper (green), from measurements in the local Universe with Cepheids + Supernovae (blue) and from the Planck analysis of the CMB (red). The measurements with UCS were combined with either cosmic chronometers (UCS + CC), the density of gamma-rays (UCS + \gamma ), or the cosmic large-scale structure, measured with weak lensing (UCS + LSS). The UCS measurements agree with the Planck estimate and are in slight tension with the measurement in the local Universe. Figure created with data from Table 1 in the paper.
So how do we solve the Hubble tension?
The authors do not provide a new model that could solve the Hubble tension. However, they show that the most favoured solutions – new physics in the early Universe – cannot remove the problem. So the Hubble tension keeps getting more mysterious!
Other independent techniques to measure the Hubble parameter, such as gravitational time delays or gravitational waves, could shed light on the matter. Upcoming new cosmological surveys, such as LSST (first light scheduled for October 2022) or Euclid (scheduled launch 2022), are even more exciting. So, as always, stay tuned for new results!
Astrobite edited by Brent Shapiro-Albert.
Featured image credit: NASA / WMAP Science Team