Title: “Cosmic Velocity Field Reconstruction Using AI”
Authors: Ziyong Wu, Zhenyu Zhang, Shuyang Pan, Haitao Miao, Xiaolin Luo, Xin Wang, Cristiano G. Sabiu, Jaime Forero-Romero, Yang Wang, Xiao-Dong Li
First Author’s Institution: School of Physics and Astronomy, Sun Yat-Sen University, Guangzhou 510297, People’s Republic of China
Status: Accepted for publication in ApJ [open access on arXiv]
Going with the (Hubble) flow?
Hubble’s law is a beautifully simple statement: a galaxy caught in the “Hubble flow,” moving with the expansion of the Universe, should be traveling away from us at a speed proportional to its distance. Unfortunately, however, this velocity-distance relation is too good to be true: due to the pesky influence of gravity, Hubble’s law is invalid in the vast majority of cases. In general, a galaxy’s net motion can be attributed to a combination of the Hubble flow, the galaxy’s motion within its galaxy cluster or group, and the motion of the cluster or group itself. We collectively refer to these deviations from the Hubble flow as “peculiar motions” or “peculiar velocities.”
While the presence of peculiar motions spoils the simplicity of Hubble’s law, these motions can be a blessing in disguise: since diversions from the Hubble flow are caused by gravitational interactions — and therefore by the presence of matter — peculiar motions serve as excellent probes for the physics of structure in the Universe. Peculiar velocities have been used to map the cosmic web — the vast network of filaments connecting matter on the Universe’s largest scales (explored further here, here, and here) — and are linked to the dynamics of galaxy clusters and the cosmic microwave background via the kinematic Sunyaev-Zel’dovich effect. Peculiar motions are also the root cause of redshift-space distortions, and thus one requires precision measurements of peculiar velocities in order to test cosmological models using the Alcock-Paczynski effect (see here and here for deeper explanations of this technique).
One caveat, though: measuring peculiar velocities is hard. To decouple peculiar motions from the Hubble flow observationally, we need a means of measuring distances that doesn’t require redshifts. To this end, a distance ladder or the Tully-Fisher and Faber-Jackson relations are viable methods, but each carry significant measurement uncertainty. Alternatively, we can take a theoretical approach, using perturbation theory to infer cosmic velocities from cosmic density data. However, any attempts to fully model the nonlinear growth of large-scale structure by hand quickly become prohibitively complex, necessitating a number of approximations and simplifications. How, then, can we accurately and efficiently compute peculiar velocities on cosmological scales? The authors of today’s paper may have found a solution in the field of machine learning: convolutional neural networks.
From Convolutions to Cosmology
Artificial neural networks are, in essence, models with very many free parameters. As one “trains” the neural network by feeding it many input data sets and scoring its output against the expected results, the network adjusts its parameters, thus “learning” how best to map the given inputs to the desired outputs. Figure 1 shows a simple neural net with a fully-connected three-layer “feed-forward” architecture; the data, in the form of an array of real numbers, is reprocessed as it’s transmitted from the “input layer” to a “hidden layer” and finally to the “output” layer. Each connection between layers bears a “weight” that dictates how a layer’s “neurons” should process their inputs — these weights are the free parameters in the neural network. Ultimately, neural nets produce models that are highly nonlinear, thus making them ideal for studying the complex dynamics of cosmic structure formation.
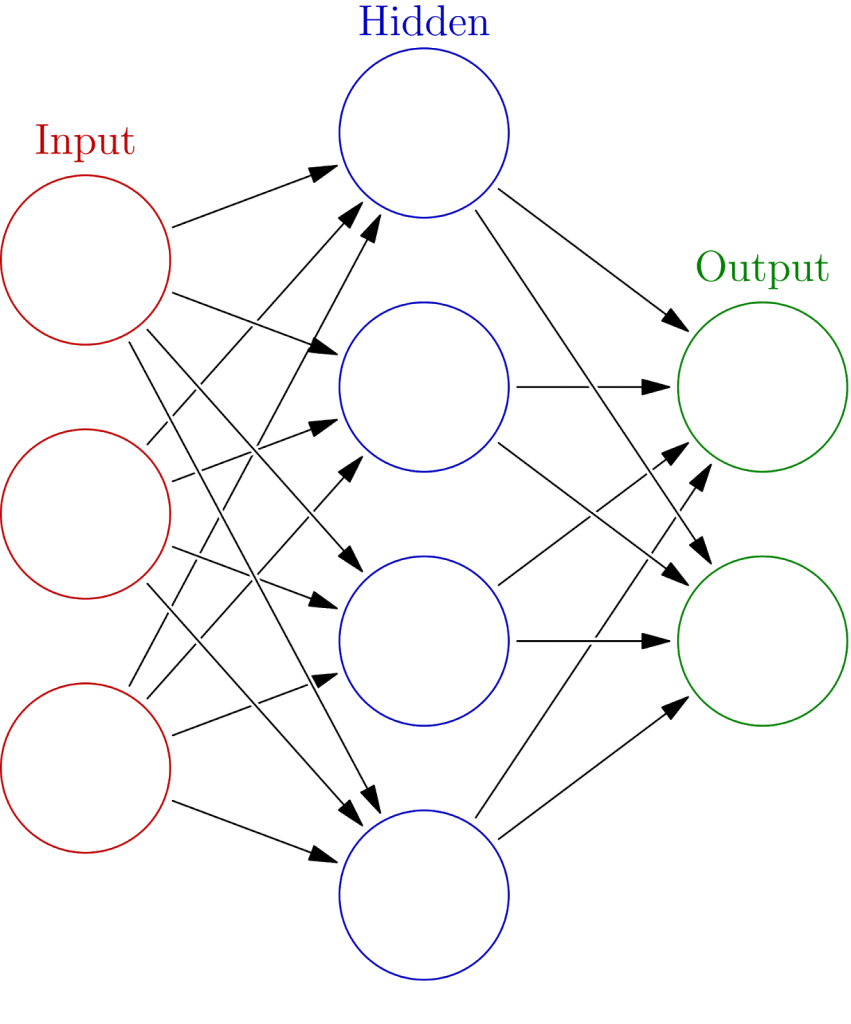
Typically, neural networks contain many hidden layers, and thus possess an obscene number of parameters — in this paper, the authors use a network with 48,690,307 parameters! With this many parameters, neural nets run the risk of overfitting the data, of using up a large amount of memory, and of running extremely slow. Fortunately, one can ameliorate these issues by adding one or more “convolution” layers to a network, filtering and contracting the data and preserving only the most salient features (for a more thorough explanation of this convolution process, see here); this is especially useful when processing detailed image data, such as the cosmic density maps that the authors use as their input data. The authors optimize their network by adopting a U-Net architecture, which employs a series of convolutions followed by a series of deconvolutions to quickly parse the input and highlight its key components.
To generate their training and testing data sets, the authors simulate the formation of large-scale structure up to the present day, retrieving both cosmic density and momentum maps; the density maps are used as inputs to the neural net, while the corresponding velocity maps — computed by dividing the momentum fields by the density fields — are used to evaluate the neural net’s output and to subsequently train, cross-validate, and test the resulting model.
Math vs. Machine
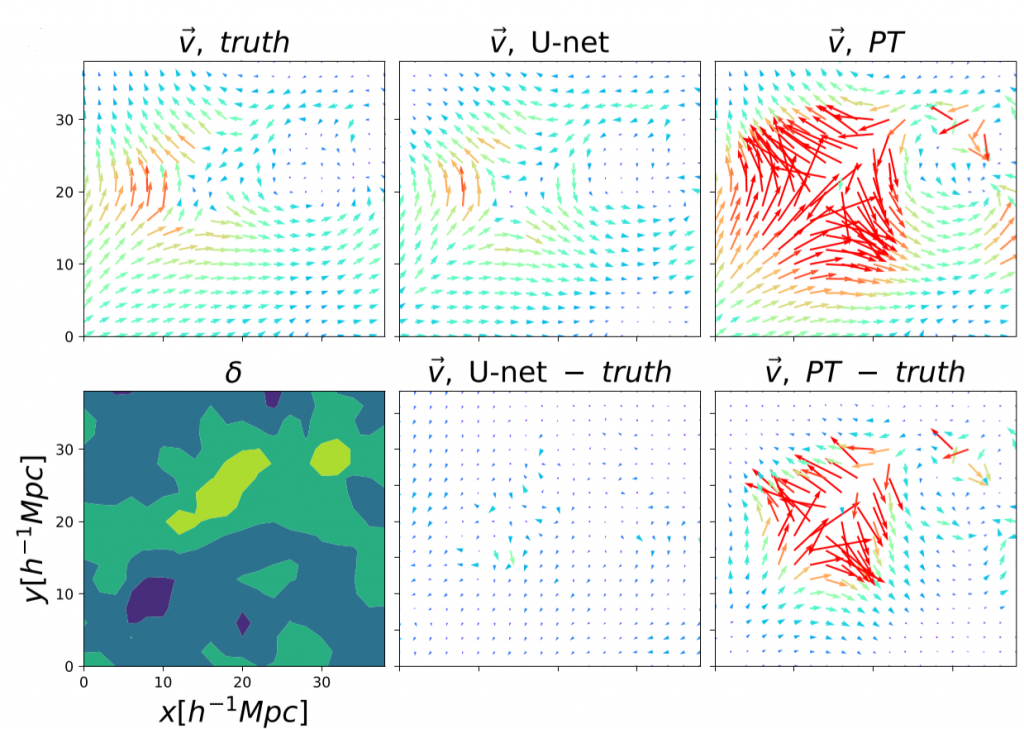
The authors assess the performance of their trained neural network by comparing its peculiar velocity predictions to those of linear perturbation theory. In nearly all cases, the neural net clearly outperforms the theoretical model. Perturbation theory performs well in regions of low density and velocity, occasionally yielding better predictions than the neural net. However, in regions of high density and velocity and in merger situations where two regions of opposing velocity collide with one another, perturbation theory fails completely, while the neural net still faithfully reconstructs the velocity field (see Figure 2). Over multiple testing data sets, the neural net is shown to be robust in all situations, while perturbation theory becomes practically useless in the presence of nonlinear dynamics.
While the neural network used in this paper can definitely be improved — perhaps by further optimizing its architecture or by using more training data — the authors have shown that neural nets can be valuable tools for predicting peculiar velocities. With such programs as DESI, EUCLID, the Rubin Observatory, and the Nancy Grace Roman Space Telescope promising to map out an unprecedented volume of the cosmos within the next decade, it is of utmost importance that we possess fast and accurate methods for parsing the new data — and neural networks are surely at the forefront of these methods. Maybe the rise of machines isn’t such a bad thing after all!
Astrobite edited by Pratik Gandhi
Featured image credit: Ziyong Wu et al. (2021)