Title: Precision Cosmology with voids in the final BOSS data
Authors: Nico Hamaus, Alice Pisani, Jin-Ah Choi, Guilhem Lavaux, Benjamin D. Wandelt, and Jochen Weller
First Author’s Institution: Universitäts-Sternwarte München, Fakultät für Physik, Ludwig-Maximilians Universität, Scheinerstr. 1, 81679 München, Germany
Status: Prepared for submission to JCAP
When studying something gets too hard, sometimes the answer is to study nothing. Modeling the nonlinear dynamics of halos and galaxies to improve our current understanding of cosmology is really hard. To a-void this problem, the authors of today’s paper use an unusual kind of (almost) nothing, cosmic voids, to learn about cosmology instead. They find some of the tightest cosmological constraints using voids so far, and they can do it without any model calibration!
What do voids have to do with cosmology? Don’t cosmologists care about galaxies and halos? What is cosmological model calibration? Let’s find out!
The voids we’re looking for
Cosmic voids are the low-density regions of the Universe that lie between the dense, collapsing structures of the cosmic web. To understand them, it pays to first think about our old friends, dark matter halos. Whereas dark matter halos are defined by how much more dense they are than the background density of the Universe, voids are defined by how much less dense they are. Halos pull matter via a net inflow toward their centers, but that matter has to come from somewhere. That somewhere: voids, which produce the necessary net outflow of matter. As a result, voids have not only much less dark matter, but also less gas and, therefore, fewer galaxies.
In practice, since cosmologists can’t see dark matter, both halos and voids are defined by galaxies that trace the underlying dark matter. Today’s authors find a void by searching for local minima in the galaxy distribution, and then defining a 3D-shape around this minimum whose edges are a pileup of galaxies (think a filament). Voids themselves are (biased) tracers of the dark matter. For the purposes of cosmology, they are analogous to galaxies living in halos. Ever the individuals, each particular void will have a different shape in general. Still, due to the homogeneity and isotropy of the Universe, on average, void profiles are spherical, as seen from the void center. However, we cannot travel to voids and measure their size from the inside, so what happens when we look at them from Earth?
Stretching out into redshift space
When cosmologists observe a galaxy’s position, what they really measure are three numbers: two angles and a redshift. The redshift contains two contributions. The first is due to the expansion of the Universe (which is accelerating due to the cosmological constant). But, the redshift also gets a contribution from the Doppler effect due to the galaxy’s peculiar velocity produced by gravitational dynamics. There is nothing weird about this velocity; the term “peculiar” is just there to distinguish it from the velocity due to the expansion of the Universe. Due to the Doppler shift, the redshift of a galaxy changes, while its angular position remains the same. Consequently, the edges of a void get stretched in the parallel direction (along the observer’s line of sight) while the edges in the perpendicular direction remain unaffected. Decoding some jargon, cosmologists say that the original (unobserved) sphere lives in “real” space, while the stretched sphere that we observe lives in “redshift space”. They call these type of effects “redshift space distortions” (RSD).
We see this stretching of a spherical void in Figure 1. The quanties used for constraining cosmology are the displacement between the void center and its constituent galaxies. In real space (lower left) the separation vector r is simply the difference between the void center position X and galaxy position x. However, when we go to the observed redshift space positions, the redshift space displacement s now depends on both the peculiar velocity of the void V|| and the galaxies v|| (more specifically, the difference components of these velocities along the observer’s line of sight). This stretching must be accounted for when constraining cosmology using voids, and is quantified in today’s paper through the parameter fσ8(z).
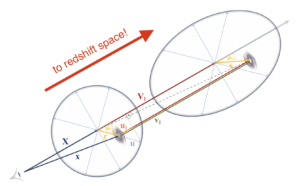
Figure 1: Schematic of how a spherical void would be affected by the transformation from real space to redshift space. Here capital letters are vectors associated with the void and lower-case letters are associated with the test galaxy. Adapted from Figure 1 of today’s paper.
The AP test – tangling with angles
Before we can talk about cosmology, we need to talk about distances. Cosmologists can infer cosmological parameters by measuring statistics of the matter distribution (e.g., the power spectrum). However, these statistics depend on the (comoving) distances between galaxies, and from observations we only know their angles and redshifts. To convert from the observed angles and redshifts to distances, cosmologists need to assume a cosmological model. Specifically, there are two distances in today’s paper – the line-of-sight distance (derived from the Hubble parameter, H(z)), and the angular diameter distance DA(z).
Since the Universe is homogeneous and isotropic on large scales, we expect that the cosmological expansion stretches a sphere by the same amount in the directions parallel and perpendicular to the line of sight. By comparing the parallel distance (after accounting for RSD stretching) to the angular (or perpendicular) distance, we can check if what we get out restores the spherical symmetry or not. If not, then we used the wrong cosmology to compute our distances and should correct for it. This check is called the “Alcock Pacynski test” (for a great intro of the AP test using voids, see this bite). The parallel distance is inversely proportional to H(z) and the perpendicular distance is proportional to DA, so DA H(z) measures the ratio between the distances – i.e. how distorted our sphere is. The AP test then informs what values of DAH(z) are consistent with undistorted spheres (averaged voids) in the data.
Results
The authors run an MCMC posterior analysis to derive constraints on fσ8(z) and DA H(z) using galaxies from the final data release of the Baryon Oscillation Spectroscopic Survey (BOSS). In particular, they take the measured redshifts and angles, assume an initial cosmology to get distances, compute void-galaxy correlation functions, and compute the likelihood before running MCMC to get posterior constraints. Similar to the usual galaxy-galaxy correlation function, the void-galaxy correlation function describes how much more likely it is to find a galaxy at a certain distance from a void center, compared to pure chance. The parameters fσ8(z) and DA H(z) are included in the model, so RSD and the AP effect are consistently included.
Results from this analysis are compared to other measurements using voids in Figure 2. The constraints of today’s paper (black triangles) are extremely competitive both for DA H(z) and fσ8(z). By default (solid error bars), the authors do not take the usual approach of fixing some model parameters by matching measurements from simulated mock data. The cosmological parameters for mock data are known ahead of time, so adjusting the model (in this case for the void-galaxy correlation function) in order to better recover these parameters is called model calibration. When employing this strategy (dotted error bars), today’s authors find tighter constraints on fσ8(z) similar to recent measurements from other analyses. However, the authors caution that they find evidence of bias in their posterior constraints when taking the model calibration approach.
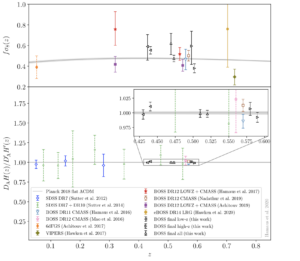
Figure 2: A compilation of cosmological measurements as a function of redshift using voids in various analyses and datasets. Top: Measurements of fσ8(z), which quantifies the growth of structure along the line of sight. Bottom: Measurements of DA H(z), the combination of angular diameter distance and Hubble parameter used in AP, normalized by the value inferred from the Planck 2018 analysis (If it is equal to one, the measurement agrees with the cosmological parameters measured by Planck). For the results of today’s paper, “low-z” and “high-z” refer to subsamples of the full dataset, with combined constraints given by the “all” markers. Measurements with solid errorbars were not calibrated using mock data. Figure 18 of today’s paper.
A future de-void of doubt?
Today’s paper and others like it show that voids are quickly maturing as state-of-the-art cosmological probes. Beyond the results on standard ΛCDM cosmological parameters as detailed by today’s paper, voids are uniquely positioned to shed light on questions of modified gravity and neutrino physics. As data from even bigger spectroscopic surveys like DESI and SPHEREx start rolling in, voids are posed to take us on an ever more informative journey through the cosmos. Bon void-age!
Astrobite edited by: Laila Linke
Featured image credit: Today’s paper