Title: Stellar activity mimics a habitable-zone planet around Kapteyn’s star
Authors: Paul Robertson, Arpita Roy, Suvrath Mahadevan
First author’s institution: Department of Astronomy and Astrophysics, The Pennsylvania State University, USA
Status: Published in Astrophysical Journal Letters
Artist’s impression of a super-Earth orbiting a small cool star. Credit: ESO/L. Calçada
If you think the Earth is old, maybe it is time to think again: in 2014, a study by Anglada-Escudé and collaborators (hereafter A14) reported the detection of two super-Earth exoplanets orbiting Kapteyn’s star, a 10 billion years-old nearby star. It is, in fact, a so-called halo star, which means it has a very eccentric (elliptical) orbit in the Milky Way. These planets (named Kapteyn b and c) were found to have orbital periods of 48.6 and 121.5 days, respectively, putting Kapteyn b inside the habitable zone (HZ) of the system.
Kapteyn’s star is an M dwarf type, which means it is cooler than the Sun. It is also very small, with only 28.1% of the mass of the Sun. Both aspects are very interesting in the search for exoplanets: 1) since a cooler star has a HZ located closer to it, it should be easier to find a habitable planet orbiting an M dwarf star than it would be for hotter stars; 2) a low-mass star is prone to higher amplitude oscillations in its radial velocities (RVs, the method used by A14) due to gravitational interaction with a planet, which again makes it easier to detect exoplanets around it.
Let me guess: somebody stole your exoplanet
The authors of today’s astrobite paper argue, however, that the detection of exoplanets in Kapteyn’s star could actually be an artifact caused by stellar activity. Using the same publicly available HARPS spectra and some of the HIRES spectra obtained by A14, the authors analyze spectral lines which are highly sensitive to stellar activity in M dwarfs, along with the results presented by A14, and some photometry data.
The first part of the analysis consists of finding the characteristic periodic signals that might appear as RV variations. They found that almost all tracers show a clear period centered at 140 days, and further analysis with HARPS data show that the actual period is 142.9 ± 0.3 days (see Figures 1 and 2), with an amplitude of about 4%. The authors conclude that this is best explained by the period of rotation of the star.
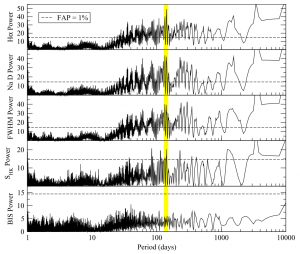
Figure 1: The periodograms show a power (measurement of how probable a periodic signal is) peak at ~140 days, interpreted as the rotation period. The other peaks are probably aliases from the rotation period.
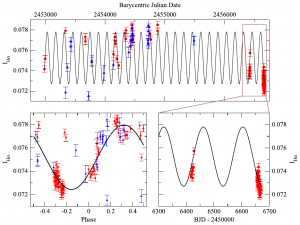
Figure 2: The data points of activity index in function of time are fitted to a sinusoidal curve that represents variations with a period of 143 days.
This period of rotation is too close for comfort to the orbital period of Kapteyn c, and almost exactly 3 times the period of Kapteyn b, which means the RVs could be correlated with stellar activity. An individual analysis of each planet’s contribution to the RVs show that the 48-day signal of Kapteyn b is highly correlated with an activity index. Other indices also show a correlation, but they could not find correlations between the RVs and photometry data.
The authors argue that the sampling cadence of the HARPS times series is the most probable cause for the planet-like signal on the RVs at 48 days, because the time windows allowed for power from the rotation period (i.e. the activity) to “leak” to shorter periods. This interpretation is also supported by previous HARPS data from 2003-2009.
Previous studies showed that it is perfectly possible to have planets around M dwarf type stars, so it is reasonable to assume planets might be orbiting Kapteyn’s star. Anglada-Escudé and collaborators have since submitted a paper to The Astrophysical Journal making a rebuttal of today’s astrobite paper, and they make a very compelling case in favor of the existence of the planets. But perhaps that should be the left for another astrobite to explore.
