Authors: R. S. Beckmann, J. Devriendt and A. Slyz
First Author’s Institution: Sub-department of Astrophysics, University of Oxford, UK
Status: Submitted to MNRAS, open access on arXiv
Supermassive black holes — the phenomenal engines that power the brightest objects in the universe, quasars — are observed only moments (ok, a few hundred million years) after the Big Bang. These observations present a major problem for astrophysics: how can these supermassive objects grow so large in such a short space of time?
There are a few competing scenarios for the formation of supermassive black holes, or SMBHs. One is that they could form from the deaths of the earliest stars, which in the pristine environment of the early universe (before all those messy metals came into existence) could have been hundreds of times the mass of the Sun. The resulting black holes would be big, perhaps up to 500 solar masses, but certainly not supermassive. A particularly vigorous growth spurt would be required to get them bulked up enough to explain observations.
A second possibility is that, in the dense environments of stellar clusters, massive stars could end up mashing together to form “intermediate” mass black holes. These would be in the range of a few hundred or thousand solar masses.
The third option is for black holes to form directly from gas in the early universe, bypassing the whole being-a-star thing and collapsing into enormous, 105 solar mass monsters which barely need to grow at all in order to become the SMBHs we all know and love in the centres of galaxies around us today.
A critical factor in working out which of these scenarios is most likely is our understanding of how black holes grow. And it’s complicated. The main ingredient is gas, but funnelling that gas into a black hole depends on processes spanning orders of magnitude in distance, from the megaparsecs-wide large scale structure of the cosmic web down to the relatively miniscule intricacies of gas falling into the event horizon of a black hole as small as our own solar system. Creating a simulation that can explore this detail as well as taking the largest structures in the universe into account is, as the authors of today’s astrobite put it, a “tremendous computational challenge”.
Many simulations tackle this by economising where they can, “zooming-in” (see Figure 1) on individual galaxies embedded in a lower-resolution universe. Even so, modelling the hydrodynamics of gas around a black hole requires far finer detail than the best resolution of large-scale simulations can achieve. This detailed physics is left to so-called “sub-grid” models, meaning that instead of increasing the resolution and working out each step according to the fundamental physics, a broader model is put in place that approximates the situation — which is much less computationally demanding.
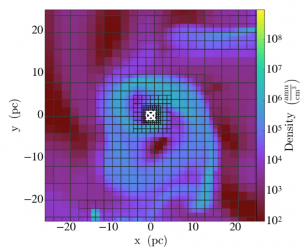
Figure 1. Zooming in on the regions of interest… the grid is adaptively refined to higher and higher resolution around the black hole, focusing computing power where it is needed most. From Figure 3 in the paper.
These crude algorithms are based on simple models of the physics of accretion, working with what can be resolved: the large scale properties of the host galaxies. While sub-grid models are a necessary evil that make cosmological simulations possible, they may have undesired effects if they are based on faulty assumptions.
Using new algorithms that make much higher resolution possible at reasonable computational costs, the authors of this paper investigate the accretion of gas onto SMBHs in much more detail than usual simulations, in order to answer the question of whether the most frequently used sub-grid models are doing an accurate job.
An important question is what effect the resolution of a simulation has on its outcome: does a coarser view of black hole feeding miss out crucial details of its growth? Figure 2 illustrates the results of both the lowest and highest resolution simulations in the paper. In their lowest resolution runs, the authors find that a SMBH grows by continuously swallowing clumps of gas in “chaotic” accretion, with the gas randomly oriented around the black hole. However, in the higher resolution simulations, a thin disc of gas forms around the black hole from which it feeds episodically, in bursts of growth. Simply increasing the resolution of the simulation drastically changes the physical processes that are observed.
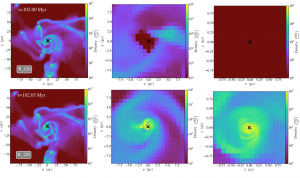
Figure 2. Densities of gas in the low resolution (top) and high resolution (bottom) simulations. From left to right, the panels zoom in on the black hole, marked with a cross. In the high resolution simulation, the gas has formed a disc around the black hole, unlike in the low resolution run. From Figure 12 in the paper.
Their simulations also show that the rate at which a black hole can grow depends strongly on the structure of the gas clouds in the immediate neighbourhood, more so than on the black hole’s mass or the larger scale properties of the galaxy. They show that even a very small seed black hole can accrete rapidly given the right gas dynamics, and catch up with black holes that started out at much larger masses. Distinguishing then between the three scenarios of black hole formation in the early universe becomes even more challenging. It also poses the problem that the most commonly used sub-grid models use the black hole mass as an input parameter — even though, as shown here, the later evolution may be independent of its initial mass.
While the authors emphasise that they investigate only an idealised case — notably not taking any feedback into account — they can use the results to comment on how to use sub-grid models to effectively reproduce the evolution that they observe in their high resolution simulations. The take-home message is that the simplest models, which require the fewest assumptions, are usually the best.



It’s my understanding that because of General Relativity, an object falling into a Black Hole undergoes time dilation because of the intense gravitational field it experiences. This is time dilation with respect to the rest of the Universe as Observer. Accordingly, the object appears to slow to a stop (relative to the Event Horizon, and again, as observed by the rest of the Universe) and cannot reach the Event Horizon in finite time (to an Observer). If this is correct, the mass that accumulates just outside the Event Horizon never becomes part of the Singularity (whatever that may be) at the Center. Such an object seems to me to be fundamentally different from the traditional Black Hole that has all its mass concentrated at the Center. Is this a valid picture? Thank you for any comments.
Hi Tom, interesting question, I’ll try to answer as best I can… I think that the important thing to emphasise is “to an observer”. You are right, a distant observer will never see something cross the event horizon – the event horizon is defined as where the escape velocity equals the speed of light, so no light (or information) from beyond the event horizon will ever be detected by your observer. However, in the reference frame of the object falling into the black hole, crossing the event horizon is no big deal and happens in a finite amount of time. So it becomes a question of your frame of reference. There’s a nice visualisation of “falling into a black hole” here – I recommend digging through those pages for some further explanation, especially the collapse to a black hole page!
In the context of this paper though, the only important thing is that there is a concentration of mass. So in the centre of a galaxy, a supermassive black hole is an incredible concentration of mass, which has an effect gravitationally on its surroundings. The modes of accretion simulated in this study, for example the nuclear disc, must necessarily occur on scales larger than the innermost stable orbit (diagram here) , and the discs here are on much larger scales than the event horizon. So what happens on the event horizon itself is not of huge consequence to the results of these simulations!
Hi Joanna, and thanks very much for your response. This has been a question bugging me for some time now. I do recall reading that relative to the Falling Observer, there’s no unusual experience with time, and so the only way to resolve our two points of view is to conclude that we (the outside universe) only see an optical illusion. In reality, the Falling Observer does enter the Event Horizon at some finite value for our time. We only see the light waves coming off the falling observer; these are not the falling object itself. At some point this light becomes invisible because it approaches infinite wavelength (speed relative to us however is constant), as the Falling Observer becomes motionless. So it only means that our mechanism for sight breaks down, losing track of what’s actually going on, and that the Falling Observer actually does enter the Event Horizon. Ok, I got that.
But (I’m sorry) this leads to the next question, Is there a way to compute in our time just when the falling observer enters the Event Horizon?
So, even though the Universe does not see the Falling Observer enter the Event Horizon, it actually does occur. (I have to repeat this to myself.)
Yes, I do understand the relative space scales.
Thanks again,
Tom
Hi Tom, I re-read your previous question and thought about this a lot… so, I think the answer is no, we cannot compute when the falling observer crosses the event horizon in our reference frame, because they don’t cross the event horizon in our reference frame. In their reference frame however, even though the falling observer would not notice any change, they could work out when they had crossed it.
This is admittedly baffling, and it is tempting to throw one’s hands in the air and say, “general relativity!”. Because I’m not sure it is simply an optical illusion: if we can’t see any light from beyond the event horizon, that means we also can’t experience the gravitational field from beyond the event horizon either, since we experience gravity (according to general relativity at least…) at the speed of light as well. So for any black hole, we only experience the gravitational field of the mass that has, at some point in the past, crossed the event horizon. Think about a newly-formed black hole from the collapse of a massive star: if we were to watch the star collapse from a distance, we would never see the mass cross the event horizon either! To us in the outside universe, it doesn’t matter where the mass is concentrated, we only feel the mass as if it was at the event horizon. We have no information at all on what is contained within that boundary, and the extrapolation to a singularity is just the consequence of theory. I hope this makes some sense… again, I’ll suggest looking at this FAQ on black holes, which might provide more context. It’s certainly a lot to think about. And as for what actually happens… that’s a very complicated question to ask, and brings up the question of simultaneity in general relativity. A “finite time” is only defined as such locally, in a given reference frame – so, for the falling observer. I am by no means an expert, so I will direct you to a very nice explanation of the problem here.
I realise this might not be a very satisfactory answer to your question, but I hope at least I’ve given you some more to think about. This has certainly given me a lot to think about!
The last image of any object will be of the object at the event horizon. To an observer it will seem as though the object is frozen in place, but reality doesn’t include only that which can be seen by the observer. Light, as well as any other object with mass is not only trapped, but is pulled toward the core of the BH, at speed dependent on the mass and density of the core.
Charles and Joanna, I wrote all that well over a year ago and have come to grips with the perplexity by simply accepting that time is relative to the observer. It’s that simple, and all that talk by me illustrates how difficult it was for me to really accept. Now, it seems very simple. We just don’t experience the unfortunate demise of the traveler, but the traveler (in proper time) does. There is however an interesting conclusion, now that I’m past the relativity of it all, and that’s to realize that matter falling into a black hole does not enter the EH either. I suppose this means that all infalling matter adds mass to the BH not at the center singularity but rather at the EH, not really “inside.” I’m not sure how this idea differs from an initial formation of a BH from an exploding star. In the latter case, is the mass of the BH inside the EH, or is it also “frozen” so much that we, or our universe, will never experience it?
It’s a tricky thing to get your head around (I remember when I was replying to your comment back then, I was very confused and had to think about it a lot!) because it’s so unintuitive.
As to your question – yes I think you’re right that to us as distant observers, the mass is effectively frozen at the EH. We just can’t know what happens to it beyond that point as we will never see anything beyond the EH. But no matter whether the mass is concentrated at the centre, or in a shell around the EH, as outside observers we will experience the gravitational potential as if it is concentrated at the centre – this is Newton’s shell theorem (I think, obviously this is a Newtonian gravity description, but I am pretty sure it should hold up here too!)
Hi Joanna, I’m glad to realize we’ve both survived these weird times.
And yes, I’m aware of the shell idea. But what do you think about other ways that the distribution of mass would manifest? I’m very sure professionals are on this, but the angular momentum of rotating BH’s would be reduced by matter falling towards the EH, more than if that matter was somehow concentrated at the center singularity. But I don’t even know how that goes. Is the matter inside the EH concentrated at the center singularity, or only some of it. I know that inside the EH, spacelike becomes timelike but I don’t know what that means with regard to the distribution of matter.
I wrote all that more than a year ago and have since come to grips with the perplexity by accepting that time is relative to the observer. It’s that simple and nothing illogical.
It does however lead to another conclusion, and that is that any in-falling matter to an already formed BH never goes beyond the EH, from our time reference. Thus, mass accumulates not “in” a BH, but just outside it. This in turn implies that the moment of inertia of a BH that has attracted much matter is very different from the moment of inertia of the BH assuming all the extra matter is at the center singularity.
I’m not sure how this fact relates to the initial formation of a BH when a star goes supernova. Is it also the case there that only some of that star’s mass associated with the BH is inside the EH, with much of it still progressing there? How is it apportioned? How much in and how much out?
Thank you – very informative!
They realize low resolution images will never give as much info as high res ones. Yet the choose low res still. How can they get an accurate picture of what’s going on if the camera can’t see it. And then even if they put the high res data and things they learned into low res images. It could give false data that doesn’t exist cause the computers filling in things it thinks should be there based on a better picture. Meaning they’re have to spend even more money to verify that the simulation is right. Might as well just go high res, makes more sense than trying to save money with a simpler system that just makes you have to spend more or possibly be totally wrong…..
You’ve identified one of the big challenges of modern astronomy! Unfortunately, obtaining higher resolution (in simulations or in observations) is rarely as simple as upgrading to a better or more expensive camera or computer. When it’s said that it is “expensive”, that usually means in terms of time – either time using telescopes, or computing hours for simulations.
This paper focuses on simulations, and you’re right that by looking at galaxy evolution in low resolution (e.g. only resolving “particles” that are the equivalent of several thousand stars clumped together) we are missing a lot of the picture. This indeed could lead to “false” conclusions, and that is exactly why this kind high resolution follow up is so important – to check that the models that we’re putting in are good enough. However, it is simply not feasible to run a whole cosmological simulation at high resolution. The BlueTides simulation, for example, took 2.6 million CPU hours to complete, taking the supercomputer several months to run – for comparison, it would take a normal laptop almost 100 years to run that whole simulation! Increasing the resolution increases the amount of time that the simulation will take, so there’s a trade off between resolution and a reasonable timescale to get results and do science. We can – and do – still learn a lot from lower resolution simulations, combined with higher resolution zoom simulations like the one in this paper.
For observations, resolution is also a big challenge that is not as simple as attaching a better camera to your telescope. A telescope’s resolution depends on 1) the wavelength of light that you are observing, and 2) the diameter of the mirror. The larger the mirror, the higher the resolution – which is why world-class telescopes are so big, but you run into engineering challenges once mirrors exceed a certain size, which puts limits on getting really high resolution images, especially at long wavelengths (I’ve written a bit more about this here). One way to get around that is to connect many telescopes together in a process called interferometry, essentially extending your mirror diameter to the distance between the telescopes… but even then we are limited by how far apart we can put telescopes. The Event Horizon telescope, which obtained the first ever image of the light around a black hole last year, has an effective diameter of the size of the planet! Even without super high resolution images, we can learn a great deal about the universe, and that can also help us target objects of interest for high-resolution observations using instruments like ALMA, which have a limited field of view so cannot observe the whole sky, and are in great demand for all different kinds of astronomical observations.
I hope this explains the challenges of high resolution a bit, and shows that it’s usually not about saving money, but just about what is actually possible given the laws of physics and our current technology and engineering!