Paper Title: Mass Derivation of planets K2-21b and K2-21c from Transit Timing Variations
Authors: Maryame El Moutamid, Kevin B. Stevenson, Billy Quarles, Nikole K. Lewis, Erik Petigura Daniel Fabrycky, Jacob L. Bean, Diana Dragomir, Kristin S. Sotzenvand and Michael W. Werner
First Author’s Institution: Cornell Center of Astrophysics and Planetary Sciences, Department of Astronomy and Carl Sagan Institute, Ithaca, NY, USA
Status: Submitted to MNRAS [Open Access on arxiv]
My sister doesn’t have to do much to get me out of sorts. That’s just a power that siblings have. You might feel like you have everything figured out, that you know your path. Still, they come along and do that one little thing that pushes you off center. They might not be trying to derail your day, and sure they are family, but after what they did something is just a little bit off. Planets are no different. If we think of them as the children of the star they orbit, there are going to be little ways that planets will mess with one another. Today’s paper looks at how these innocent tugs can tell us about the character(istics) of the planets involved.
“I’m not touching you“
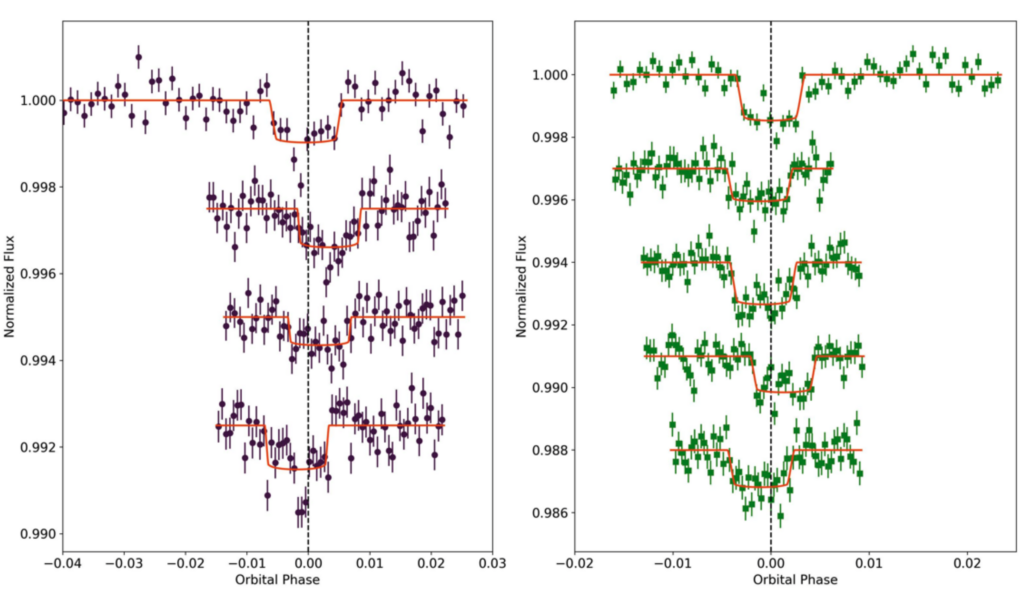
The sibling dynamic we will focus on is between the children of the star K2-21. The K2 mission found two exoplanets orbiting the star, which carried the family name and are called K2-21 b and K2-21 c. The K2 mission is extremely good at finding planets using the Transit Method. This relies on measuring the brightness of the star, and noticing a slight dip in the brightness as the planet completes an orbit. A single planet (K2-21 b) will orbit regularly, and the dips will appear at the exact same time based on how long the period is. This can tell you that the planet is there, and how big it is which will depend on the size of the dips. What it doesn’t tell you is how massive it is.
However, if there is an additional planet (K2-21 c), then it will tug on its sibling in a small but noticeable way as it orbits, and vice versa (I guess it is hard not to retaliate). This tug will slightly speed up or slow down the planet and cause it to transit just a few seconds to minutes before or after it is expected to. This is known as a Transit-Timing Variation or TTV. How off the TTV is will be based on the masses of the planets. In Figure 1 we can see the transits of K2-21 b and K2-21 c, and that they are rarely exactly where they are expected to be. This can give us information about their mass!
“They started it!“
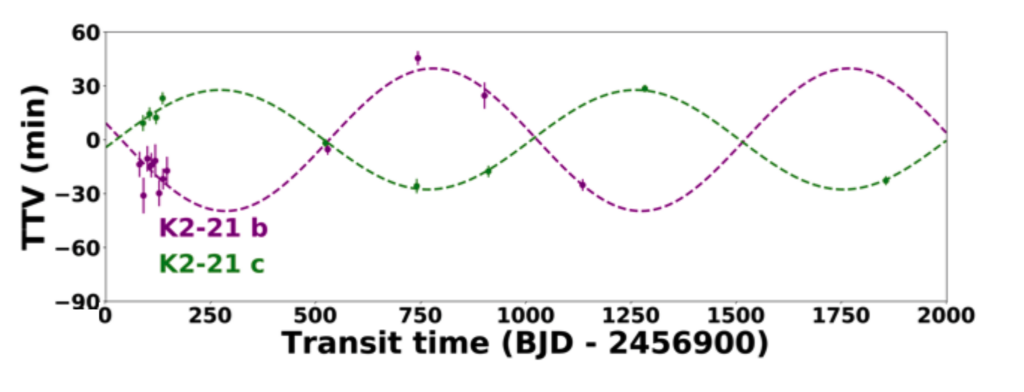
Using additional transits from the Spitzer mission, the authors modeled how massive the planets would need to be to tug on each other in the way observed. Figure 2 shows the measured TTVs compared to the model. It looks like a great fit! However, there is a large range of what the masses could be as the tug that the planets feel will be related to their relative mass, and they can’t constrain the eccentricity or shape of the planet’s orbits as well as they would like.
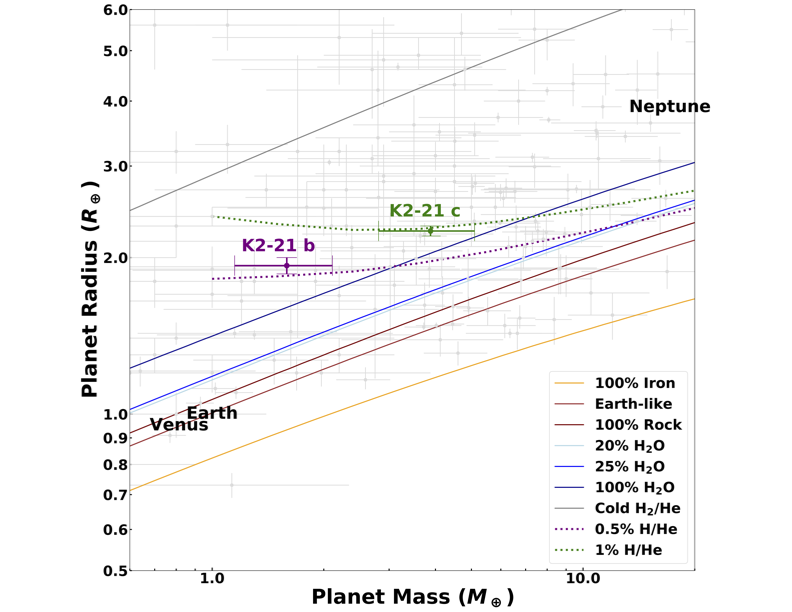
Regardless, the masses are a great first estimate, and can be combined with the well defined radii from the transit method to create an initial estimate for the density of the planets. Figure 3 shows how the size and mass of the quarrelsome siblings compares to other planets. The authors suggest they probably have atmospheres similar to Neptune, made of hydrogen and helium, with the caveat that if they are actually at the other end of large mass range from the model there is a chance they could have a more watery composition. They conclude by saying that using JWST to measure another TTV would be a great way to quickly refine their estimates.
Family Sticks Together
The gravitational effects of having a sibling planet can sometimes be off putting. In the worst case, it might even drive a planet to leave the family altogether. However, it can also be stabilizing. The authors point out that while not quite there, the exoplanet system is very near a 5:3 resonance, for every five orbits K2-21 b makes, k2-21 c makes three. Resonant orbits are extremely stabilizing, with famous examples being the moons of Jupiter and planets around Trappist-1. If siblings do know how to push buttons, it also means that they know what you need to stay in check. Once you find resonance with them, it can be one of your most enduring and rewarding relationships (love you Anna).
Astrobite Edited by Lynnie Saade
Featured image credit: Photo by Obie Fernandez on Unsplash with elements from the NASA Exoplanet Catalog




Do resonant orbits have a relationship to Bode’s Law?
Great question! Bode’s law doesn’t have a firm theoretical explanation, it’s more of an observational pattern that the spacing of planets in our solar system somewhat agrees with. Resonant orbits definite make certain orbits preferred for a planetary system to exist longterm, so a random exoplanet system will likely resemble a Bode’s law arrangement. I don’t know if it’s safe to say there is a relationship between the two, but they definitely rhyme!