Title: What can CMB observations tell us about the neutrino distribution function?
Authors: James Alvey, Miguel Escudero, and Nashwan Sabti
First Author’s Institution: GRAPPA Institute, Institute for Theoretical Physics Amsterdam, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
Status: Preprint on arXiv
The Standard Model (SM) of particle physics is hands-down the most successful theory ever. However, we know that at some level the SM is incomplete, and this is in part due to the presence of massive neutrinos. Neutrinos are fast-moving SM fermions (leptons) that interact with other particles only via weak and gravitational interactions. Neutrinos are everywhere – at least hundreds of thousands of them from the early universe are passing through your body right now! However, the SM predicts that neutrinos should have no mass, which is awkward, because particle physicists have measured their masses to be non-zero. As a result, neutrinos get to join the increasingly uncomfortable number of elephants (like dark matter and dark energy) in the beyond-SM room.
Particle physicists are trying very hard to provide an upper bound on the neutrino masses to add to the current lower bound from neutrino oscillations. The current best constraint from the KATRIN experiment is <0.8 eV (for reference, the electron mass is 511 thousand eV), but it turns out, the sum of neutrino masses can be better constrained by cosmology! In particular, the Planck Cosmic Microwave Background (CMB) and Baryon Acoustic Oscillation (BAO) data already constrain this sum to be less than 0.12 eV, and future datasets are expected to bring this upper bound even lower.
This all sounds wonderful, but today’s paper rains a bit on this parade (in a good way). Existing cosmological constraints usually (as in quoted the Planck+BAO case) assume a particular choice of neutrino physics and the Lambda Cold Dark Matter (ΛCDM) model. But what happens if we are a little more permissive in the types of neutrino physics we allow? How can we explore these choices? Today’s paper provides an answer – in *particular*, today’s paper explores how much wiggle room the CMB constraints leave on neutrino mass when going beyond the “standard” ΛCDM cosmological model.
Prepare to meet your density
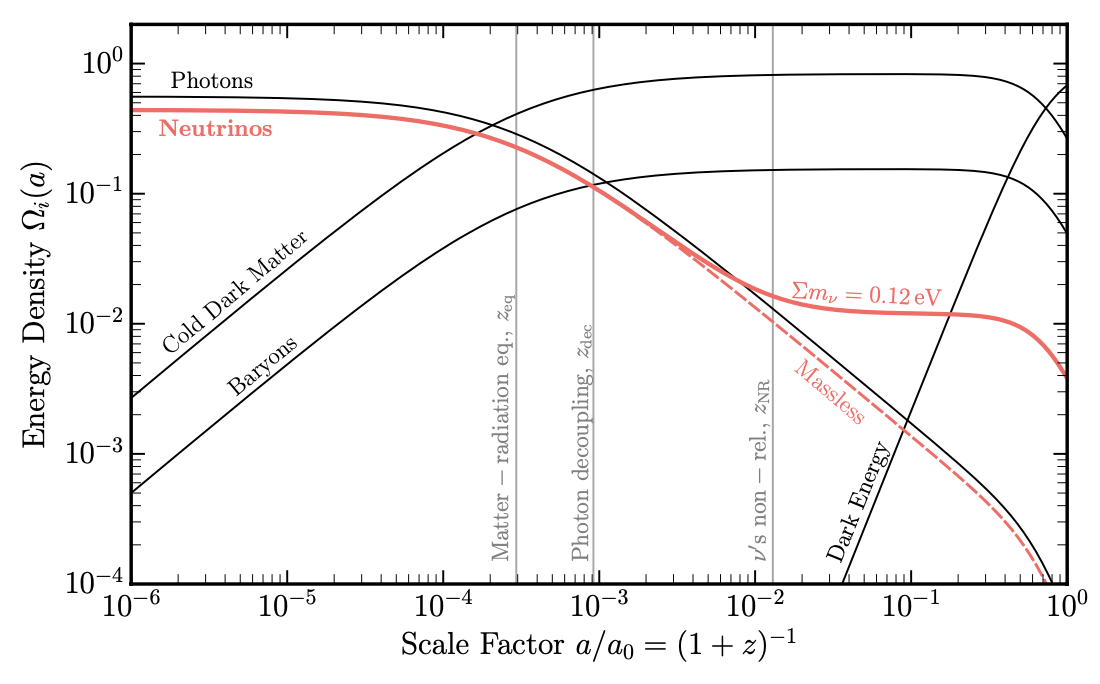
Figure 1: Time evolution of cosmological species (at the level of background dynamics) in terms of energy density. A scale factor of 1 corresponds to today, while a scale factor of 0.001 marks the time of photon decoupling associated with the CMB. The red curve illustrates how the time evolution of the neutrino energy density bifurcates at late times depending on whether neutrinos are massive or not. Figure 1 of today’s paper.
Neutrinos behave differently in the early and late universe (Figure 1). In the former, neutrinos behave like radiation and are characterized by their relativistic energy density ⍴R (the red curve looks like the nearby black one for photons), while in the latter they behave like matter (the solid red curve is similar shape to cold dark matter one) and are described by their non-relativistic energy density ⍴NR. In the middle, which unfortunately we cannot observe well, neutrinos undergo a transition from being relativistic to nonrelativistic (splitting of red solid and dashed curves in Fig. 1). The CMB data can constrain the behavior of neutrinos near decoupling (⍴R) through characteristic scales corresponding to baryon oscillations, as well as later on through the contribution of neutrinos to the background expansion of the universe (⍴NR). The BAO probes low redshifts as well, and can help constrain ⍴NR when the neutrinos are non-relativistic.
Makes neutri-no difference to me
Today’s authors consider several choices of neutrino physics models (parameterized through their phase space distribution functions) that are distinct from the standard ΛCDM choice of particles obeying Fermi-Dirac statistics. These models, for example, correspond to especially high or low energy neutrino populations that may or may not have “dark radiation” mixed into the model. For each model, the authors perform posterior inference of massive neutrino parameters using the Planck Cosmic Microwave Background (CMB) anisotropy power spectrum temperature and polarization data. This high-redshfit CMB data is then combined with low-redshift Baryon Acoustic Oscillation (BAO) data from BOSS.

Figure 2: Posterior constraints on the non-relativistic massive neutrino density (as measured today) produced using Planck+BOSS Baryon Acoustic Oscillation data. Different colored curves correspond to significantly different choices of massive neutrino physics (ΛCDM in dark blue), yet all are constrained at about the same level, indicating that the data cannot discriminate between these different models. Extracted from Figure 2 of today’s paper.
The results of this analysis for the non-relativistic energy density are shown in Fig. 2 (different model choices are the different colored curves). The exact interpretation of the non-relativistic energy itself is not particularly important here, but it is clear that all the choices of modeling give a similar constraint to the ΛCDM constraint (dark blue curve), indicating that this data cannot distinguish between the different choices neutrino physics as encoded in the different curves. With this lesson in mind, should we really be so sure of our “standard” ΛCDM model for neutrinos?
The CMB and BAO weigh in on neutrino mass
To explore beyond the standard (ΛCDM) assumptions of neutrino physics, today’s authors develop a “generalized” massive neutrino physics model. This model is flexible enough to account for neutrino masses corresponding to the previous choices that were constrained individually in Fig. 2. By using the more flexible model, the authors aim to provide a model-independent constraint on the sum of the neutrino masses, as well as the other properties to which the CMB+BAO data is sensitive. Figure 3 shows the posterior constraints on the three neutrino parameters in this model.
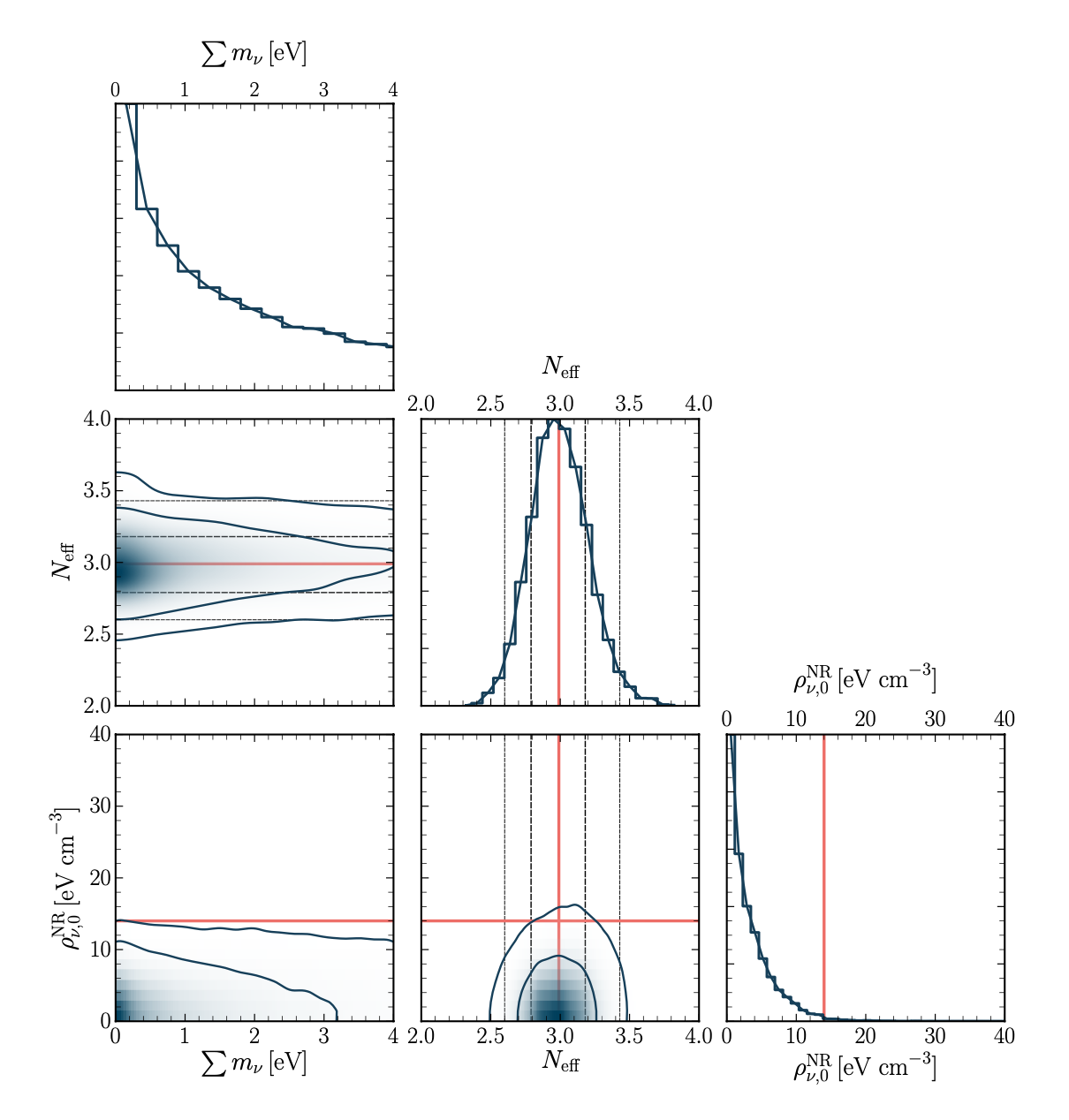
Figure 3: Posterior constraints on a subset of the parameters using Planck+BAO data and the “generalized” form of the massive neutrino model. Neff measures the (relativistic) energy density of neutrinos at early times, while ⍴NR,0 measures the (non-relativistic) energy density of neutrinos at late times. The neutrino mass is fairly poorly constrained within the range of its allowed values. Figure 4 of today’s paper.
As before, we have the non-relativistic energy density ⍴NR, but now have the parameter Neff and the sum of neutrino masses itself, rather than several choices of fixed neutrino physics model and neutrino mass (as in Fig. 2). The parameter Neff is closely related to the relativistic energy density ⍴R, and essentially just re-expresses ⍴R in terms of the photon energy density. The authors want you to take away from this plot that when the neutrino physics modeling is relaxed, not only does the CMB+BAO constraint on the sum of neutrino masses relax significantly, but the constraint on Neff is not significantly worse than the ΛCDM constraint.
A-massing more evidence
From the results of today’s paper, it seems that there is indeed more wiggle room for the sum of neutrino masses in the general neutrino physics case than in the ΛCDM case. At least from the perspective of Planck CMB and BOSS BAO data, the authors showed that the details of neutrino physics will be hidden from us for the time being. But, never fear, large-scale structure is here! As a parting comment, today’s authors suggest that future weak lensing or galaxy clustering analyses may be able to tighten neutrino mass constraints even for the generalized model considered here. Stay tuned – *nu* physics might be on the horizon!
Edited by: Jason Hinkle
Featured Image: Sanford Underground Research Facility