Title: Primordial Black Holes Arise When The Inflaton Falls
Authors: Keisuke Inomata, Evan McDonough, and Wayne Hu
First Author’s Institution: Kavli Institute for Cosmological Physics and Enrico Fermi Institute, The University of Chicago, Chicago, IL 60637, USA
Status: Preprint on arXiv
In light (or dark) of the rapidly growing number of detected black hole mergers, some astrophysicists now more than ever are asking the question: “could LIGO/VIRGO black holes be primordial?”
For black holes to be “primordial”, they have to form in the early universe, but how early in the early universe are we talking? Very early, it turns out, because the way they form has to do with inflation. In particular, the slight density fluctuations (patches of over- and underdense regions) in the early, mostly-uniform, universe are seeded by inflation. Over most of cosmic history, these fluctuations grow and are responsible for the formation of stars, galaxies, and large-scale structure in the universe today. However, if some of these density fluctuations were large enough, they could have collapsed directly into black holes. These hypothetical objects are called primordial black holes (PBHs). PBHs are distinct from “regular” black holes because they form without going through the process of stellar evolution that produces stellar-mass black holes. We’ve covered PBHs here at astrobites before (there are a plethora of great bites by Philippa Cole), and it remains a possibility that LIGO/VIRGO-mass (>10 solar masses) black holes could be primordial.
The authors of today’s paper put a new spin on the production mechanism of PBH seeds during inflation, and introduce a class of inflation models characterized by a concentrated steepening of the inflaton potential. That’s a bit of a mouthful, but we’ll do our best to unpack what it means in today’s bite!
Inflate-gate – entry and exit through the Hubble length
There are already some wonderful astrobites introducing inflation (see here and here), but to state it quickly, inflation is a period of accelerating expansion (no, not that accelerating expansion) that predates the hot big bang. It turns out that adding inflation to the evolution of the universe solves several problems that cannot be explained by the hot big bang alone.
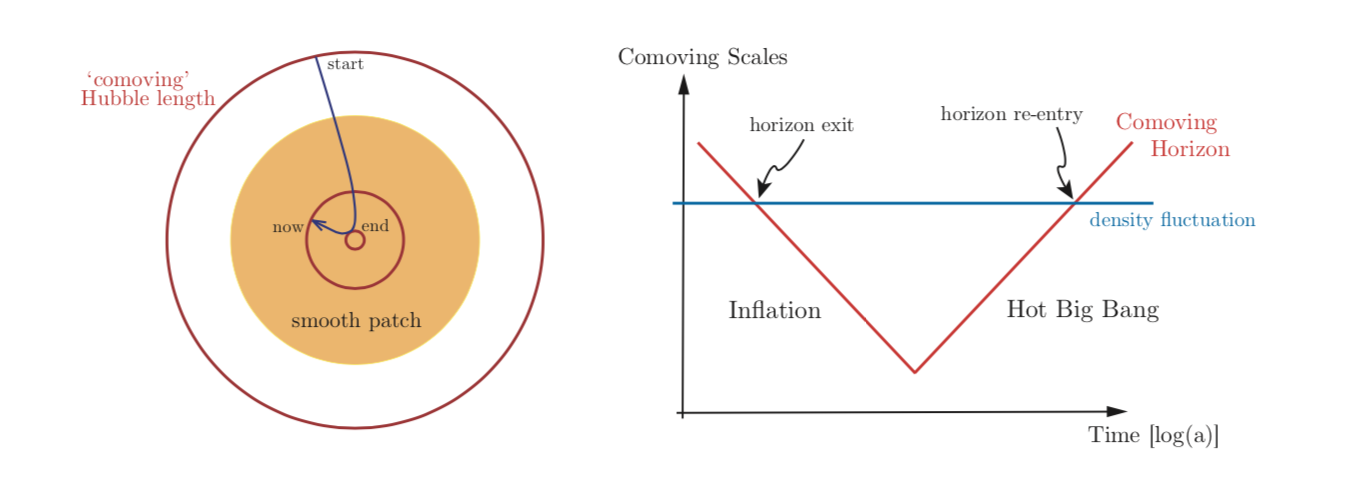
Figure 1: A schematic view of inflation in terms of the evolution of the (comoving) Hubble length. Left: Following the dark blue arrow, the Hubble length defines a sphere that shrinks during inflation until reaching its end before turning around and growing during the hot big bang. Right: A view of the same process with the fixed (comoving) scale of a particular density fluctuation overplotted, which defines its horizon exit and horizon entry points. Figure 7 of Daniel Baumann’s TASI lectures on Inflation.
We can also characterize inflation in terms of the Hubble length. The Hubble length (also sometimes referred to as the “horizon”) is the length scale outside which no two observers can communicate with each other due to the finite speed of light at a particular moment in time. We can get a feel for the Hubble length view of inflation in Fig 1. On the left, we schematically start with a sphere of size the Hubble length at some very early time during inflation. This sphere then shrinks (as the expansion accelerates) until some time, the end of inflation, where it reaches a minimum size. After this point, the Hubble length begins growing again, and the hot big bang proceeds as usual in the standard cosmological model.
An important physical implication of this evolution of the Hubble length is related to the notion of causality. In the early universe, we care about what happens to primordial fluctuations of a certain size because they are responsible for seeding the structures we see around us today. Since at scales greater than the Hubble length, no physical events can communicate, in a very rough sense, fluctuations that have a characteristic size larger than the Hubble length are “frozen” and don’t evolve in time.
So imagine a density fluctuation of some size that is smaller than the initial Hubble length in Fig. 1, but is larger than the Hubble length at the end of inflation (as shown by the blue line in the right panel). Initially, it can evolve away to its heart’s content, but once the Hubble length shrinks below the size of our fluctuation, the fluctuation freezes in its tracks. This is referred to as “horizon exit”. Inversely, once inflation ends and the Hubble length starts increasing again, our fluctuation eventually “re-enters” the horizon and thaws out, participating in causal physics again when the Hubble length is bigger than it.
You might now be asking, dear reader, – what does any of this have to do with black holes? Well, we already heard that PBHs are generated by large density perturbations in the early universe – so we need some mechanism to generate the things that generate the PBHs. Today’s paper provides such a mechanism through a model of inflationary dynamics that produces the right type of overdensity fluctuations that can evolve into PBHs in the LIGO/VIRGO mass range.
One small step for the inflaton…
Perhaps the simplest model of inflation, single-field slow-roll inflation, is an accurate model for describing the features we see in the cosmic microwave background (CMB). The key idea of slow-roll inflation is that, analogous to a ball rolling down a hill, a single field (called the inflaton) “rolls” down a potential, picking up kinetic energy in the process. To be consistent with CMB observations, this roll has to be very slow – i.e. over a very shallow region of the potential.
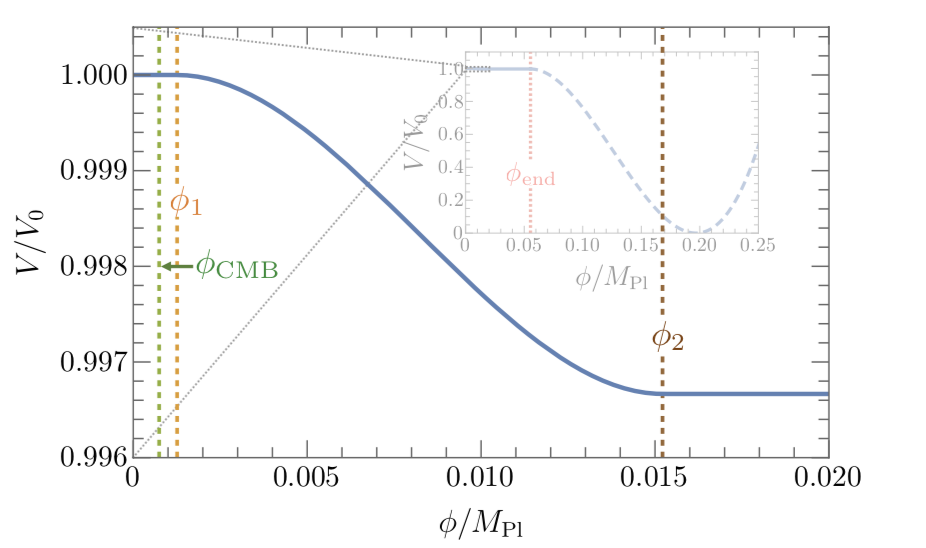
Figure 2: The inflaton potential with a concentrated steep region added to the shallow region. The extent and location (in ɸ), as well as the slope of the steep region, are the characteristic features of the model of today’s paper. Figure 1 of today’s paper.
The idea of today’s paper is to change the slow roll picture by adding a region of decreased slope in the potential, but which is very narrow in extent, followed by a very flat region of the potential. We can see this in Fig. 2, where the shallow region of the potential has a very narrow (zoomed-in) steeper portion. The authors then spend the rest of the paper deriving the consequences of such a potential, in particular by solving the equations of motion for the primordial fluctuations. The final result of this is a prediction for the “primordial power spectrum”, which is explained in this bite, and which effectively measures correlations in fluctuations at a certain scale.
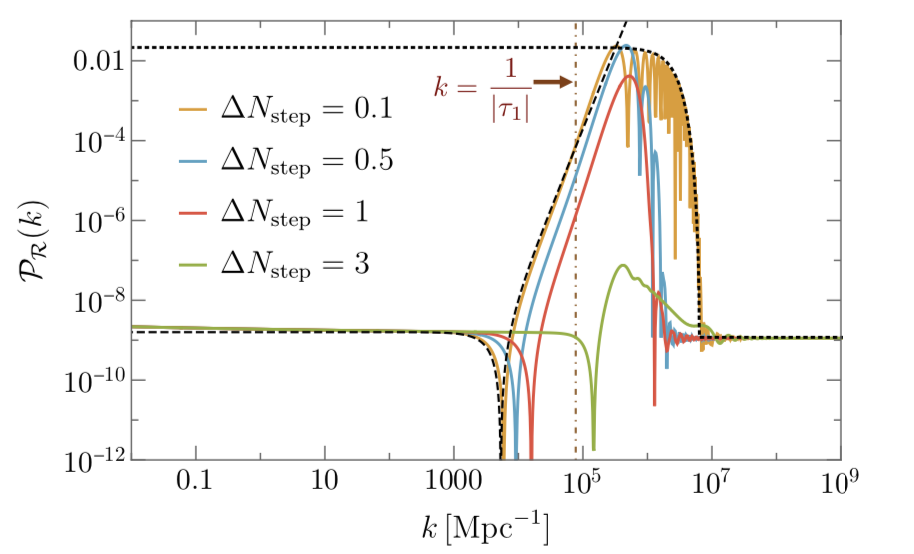
Figure 3: The primordial power spectrum in different models of the type introduced in today’s paper. All models result in enhanced power at high wavenumber k (i.e. on small scales). In this comparison, a sharper step corresponds to a feature that is broader in wavenumber and higher in amplitude than that produced by a smoother step. The vertical line marks the scale of the fluctuation exiting the horizon at the time corresponding to the steeper transition. Figure 2 of today’s paper.
The predictions for the primordial power spectrum in this model are presented in Fig 3. Here the authors have plotted the primordial power spectrum for various choices of the width of the extent of the region of decreased slope in the potential. The models all produce a feature with enhanced amplitude at large wavenumber, but give a relatively flat shape at low wavenumber, which is required observationally by the CMB. The size, amplitude, and location of this feature are determined by the particular values for the starting location of the steepening of the slope and the width of the steep region. The reason that the scales larger than these features (at lower k) are unaffected by the small steep region is that they are already frozen outside the horizon at the time when the transition occurs during inflation. The upshot of this is that such enhanced features can provide the necessary conditions for large primordial fluctuations on small scales that can serve as PBH seeds for LIGO/VIRGO-mass black holes!
Coming up on the horizon
Well, what now? More observational constraints on the PBH content of the universe at different mass ranges are constantly being released from a variety of astrophysical probes, as are forecasts for future missions that could detect their presence. The authors volunteer a specific observational test of their model, namely that their model would make the impact of gravitational waves on the CMB extremely small. As a result, the detection of the signature of primordial gravitational waves by upcoming CMB experiments such as Simons Observatory and CMB-S4 would rule it out. We’ll just have to wait and see – it’s gonna be a while, so grab a snack while you wait, maybe some PBH&J!
Featured Image: Today’s paper
Edited by: Viraj Karambelkar