Title: Observation of Gravitational Waves from a Binary Black Hole Merger
Authors: The LIGO Scientific Collaboration and The Virgo Collaboration
Accepted by Physical Review Letters
Disclaimer: I am one of over 1000 scientists in the LIGO-Virgo Collaboration. Many members have been working for decades to accomplish this feat of scientific discovery. Twelve papers were written in companion to the gravitational wave detection paper and are filled with more amazing results. This bite just scratches the surface of the implications of this discovery. See here for much more!
In 1916, the year after correctly formulating the theory of general relativity, Albert Einstein predicted that accelerating masses create ripples that propagate through the fabric of spacetime. However, Einstein himself believed that any attempts to detect these “gravitational waves” would prove futile, as the effect that they have on their environment is miniscule. Almost poetically, a century after Einstein’s prediction this elusive phenomenon has been validated. On September 14th, 2015, a new window to the Universe was opened.
Detecting a ripple in spacetime
Though gravitational waves are invisible, they do have a measurable effect on the space they travel through by causing distances to shrink and stretch. That is where the Laser Interferometer Gravitational Wave Observatory (LIGO) comes in. The LIGO detectors in Livingston, Louisiana and Hanford, Washington utilize laser light as a very precise stopwatch to measure this effect. The detectors are identical Michelson interferometers, shooting powerful lasers down equal-length cavities four kilometers in length. Since the speed of light is constant, if the race down the interferometer arms and back is a “tie” it means that the light traveled the exact same distance and the arms are exactly the same length. LIGO is set up to have the beams destructively interfere in this case, resulting in no signal in the detectors. However, if one of these arms is stretched or shrunk, say by a gravitational wave, the race will not be a tie; the beam traveling down the shorter arm will win the race and interfere with the beam traveling down the longer arm, creating a signal.
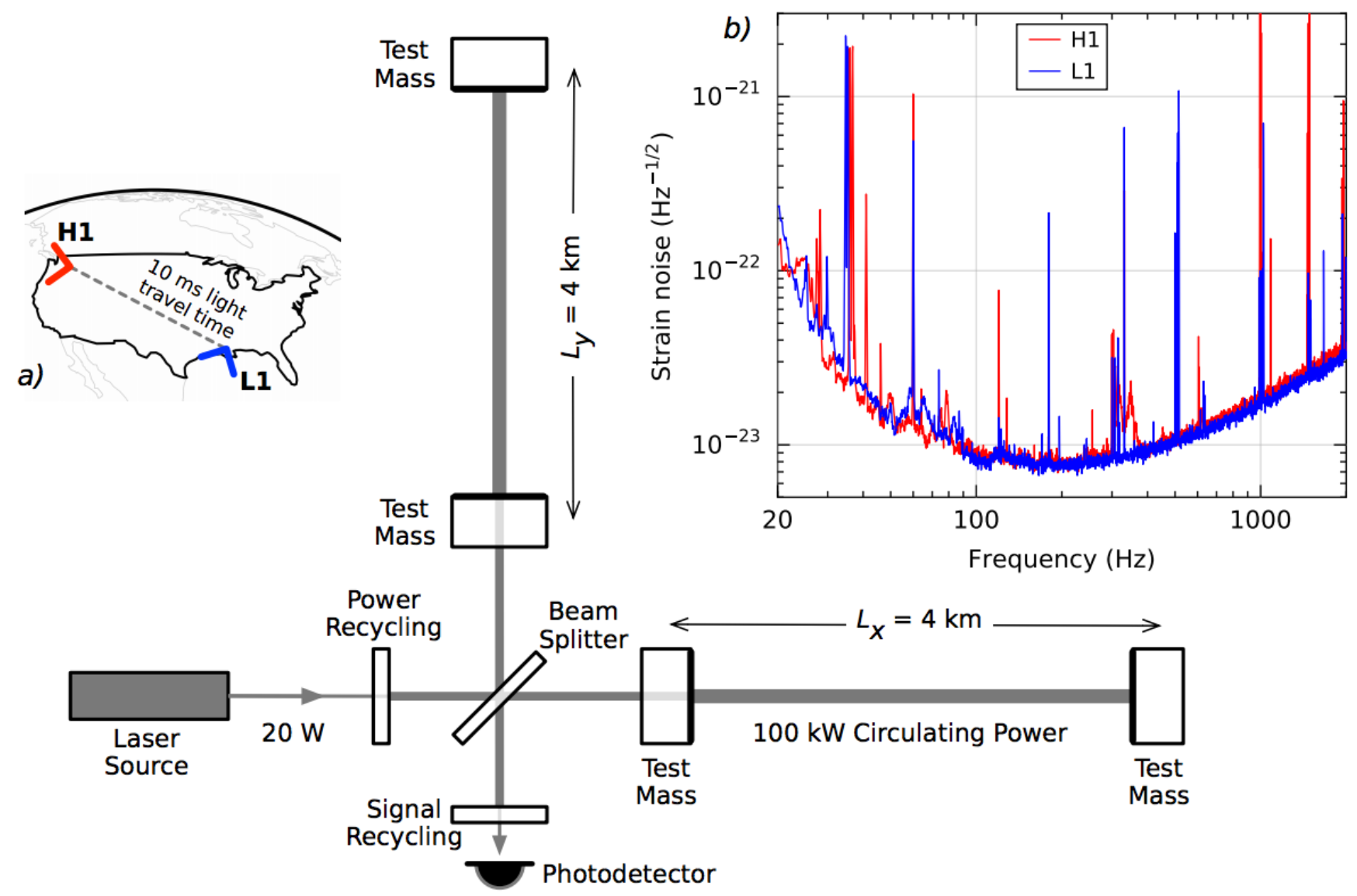
Figure 1. A simplified diagram of an Advanced LIGO detector. The upper-left inset shows the location and orientation of the two LIGO detectors, indicating the light travel time between the detectors. The upper-right inset maps the instrument noise for the Livingston (L1) and Hanford (H1) detectors. The noise is dominated by seismic activity at low frequencies and shot noise at high frequencies. Narrow spikes are caused from various sources, such as electric power grid harmonics and vibrational modes of the suspension system. Figure 3 of the detection paper.
The signal that LIGO detected on September 14th, referred to as GW150914, came from the merger of two black holes that were about 36 and 29 times the mass of the Sun. During the second before these giants merged, the energy released in gravitational waves from the system was 10 times greater that the energy released by all the stars in the observable universe! However, since spacetime is very “stiff” and the black holes merged over a billion lightyears away, even an event as powerful as this created a minuscule effect on the space that Earth occupies.
Whisper from the Universe
The strength of signals detected by LIGO is given by a dimensionless quantity known as strain, which is essentially the change in the length of the interferometer’s arms divided by the arm length. LIGO can detect strains analogous to a change in distance in the 4-kilometer-long arms that is 10,000 times smaller than the width of a proton. For another perspective of how tiny this strain is, if the length of the interferometer arms were instead an Earth–Sun distance of 150 million kilometers, this strain would only be change of distance in these hypothetical arms as small as a hydrogen atom! Over its 1/5th of a second in the LIGO frequency band, GW150914 reached a peak strain of 10-21.
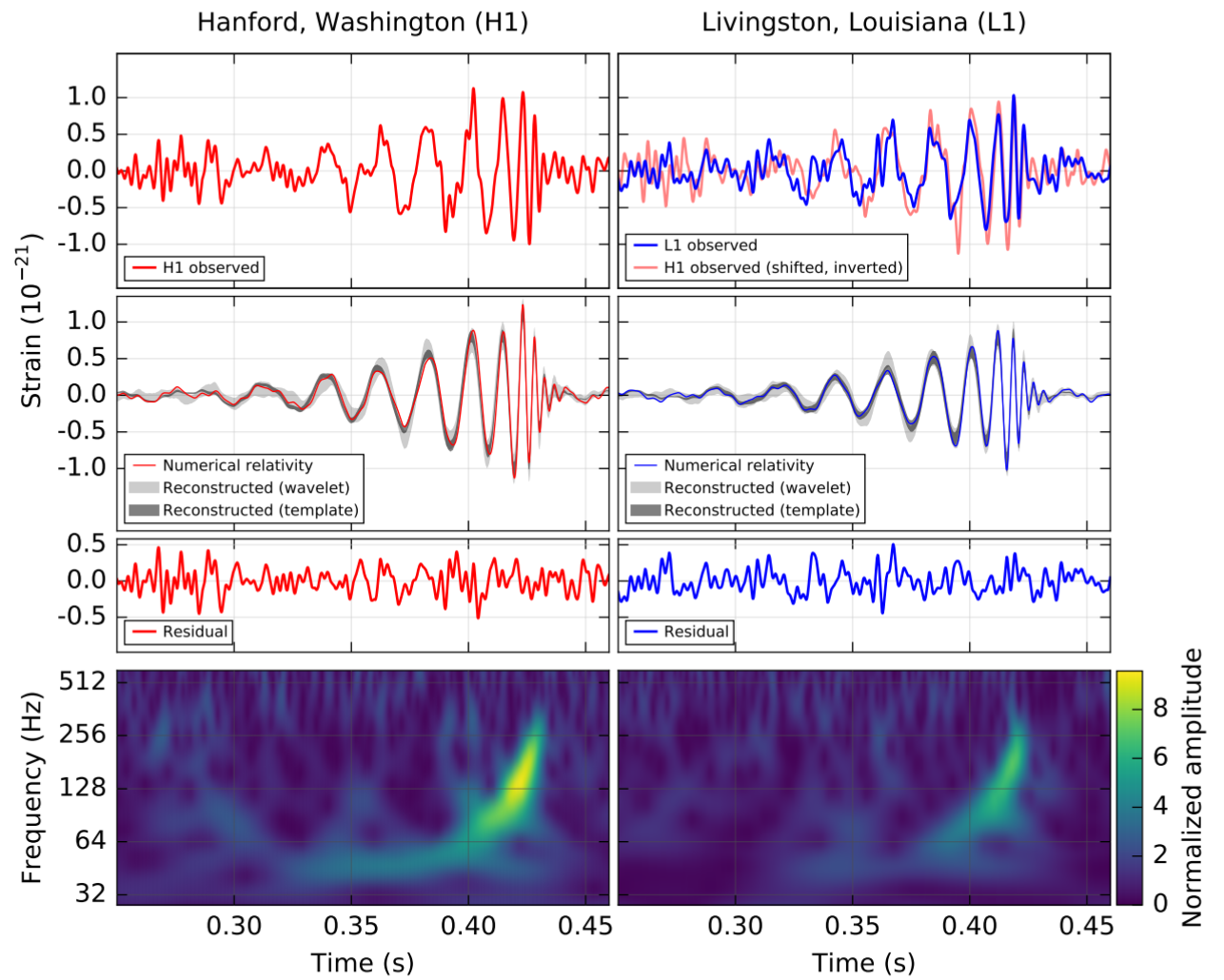
Figure 2. GW150914 observed by the Hanford detector (left column) and Livingston detector (right column). The top row shows the strain measured in each of the detectors. The second row shows the strain in the 35-350 Hz band (cutting out low and high frequencies), a numerical relativity waveform for a system with parameters consistent with GW150914 (solid line), and the 90% credible regions for two independent waveform reconstructions (gray). The third row shows noise residuals after subtracting the filtered numerical relativity waveform from the filtered detector time series data. The bottom row shows a time-frequency representation of the strain data, with the distinctive “chirp” of the signal frequency increasing over time. Figure 1 of the detection paper.
Since LIGO needs to be sensitive to the tiny signals of gravitational waves, it is also susceptible to various environmental and instrumental sources of noise. LIGO data is inherently noise-dominated. Though coherence between the two detectors is used as an initial screening (astrophysical signals are expected to be seen in both detectors with a time difference less than or equal to the light travel time between the detectors), sophisticated data analysis techniques are still necessary to search through the data for true astrophysical signals. One of the methods used involves searching for genuinely “loud” signals. However, trying to find a gravitational wave signal is like trying to hear a single conversation in a very loud party — it greatly helps to know how the particular conversation is meant to sound. Equipped with the equations of general relativity, simulated waveforms are created for thousands of compact binary merger systems. These “template” waveforms are compared to the LIGO data as another means to search for true astrophysical signals. Both of these search techniques recovered GW150914, and provided the 5-sigma confidence that is a standard for scientific discovery. This means that the rate at which a signal analogous to GW150914 is created by noise is less than 1 in every 203,000 years.
Deciphering the signal
Utilizing the waveform detected by LIGO and the best-fit numerical relativity waveforms, properties of the binary black hole system were estimated. The waveforms of binary black holes depend on 15 intrinsic (e.g. spin, mass) and extrinsic (e.g. sky location, inclination) parameters. Bayesian statistical techniques such as Markov Chain Monte Carlo estimated the mass of the black holes to be ~36 and ~29 solar masses, the redshift at which the merger occurred to be ~0.09, the final mass of the merged black hole to be ~62 solar masses (the missing 3 solar masses of energy is what was released by gravitational waves during the merger), and the sky location of the event.
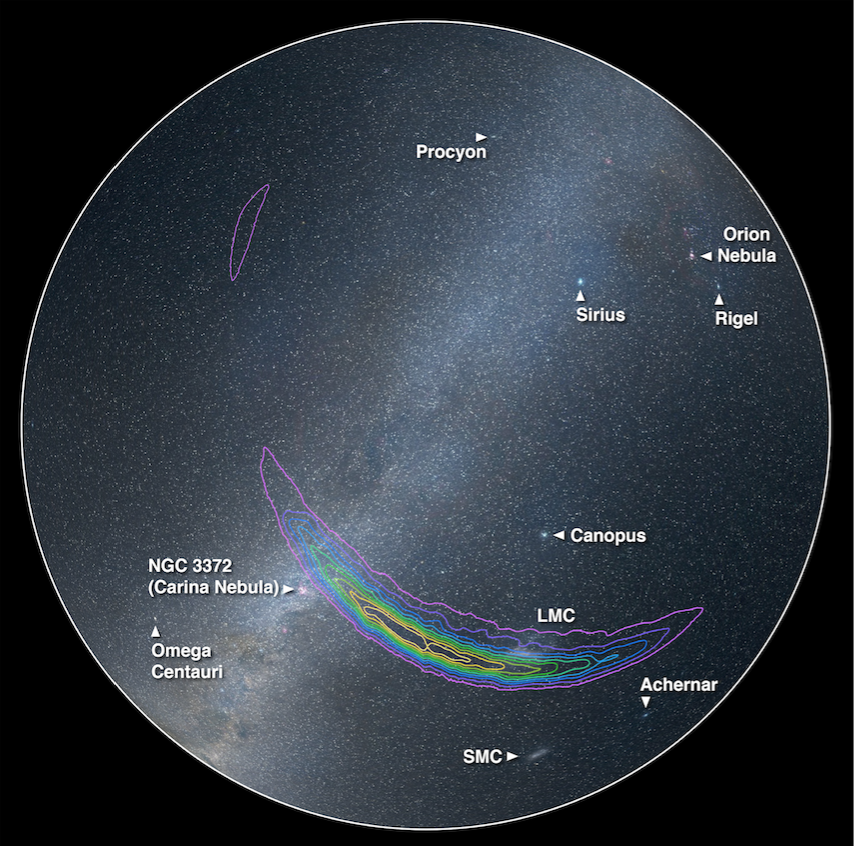
Figure 3. The estimated sky location derived from the most accurate parameter estimation code. The different colors mark 10% increases in the probability that GW150914 came from these regions. Note that we do not expect to see an electromagnetic counterpart for the merging of two black holes. Figure derived from figure 4 of the companion paper Properties of the binary black hole merger GW150914.
In addition to being the first direct detection of gravitational waves, GW150914 is loaded with astrophysical implications. This event provides the first observational evidence of binary black hole systems, and tells us that these systems can merge within the age of the Universe. GW150914 also provides the first evidence that “heavy” black holes actually exist in nature; before this discovery indirect evidence of stellar-mass black holes only uncovered masses up to ~20 solar masses. As an added bonus, GW150914 provided a unique test to Einstein’s 100-year-old theory (which passed with flying colors), as well as being the first true test of the strong-field regime of general relativity.
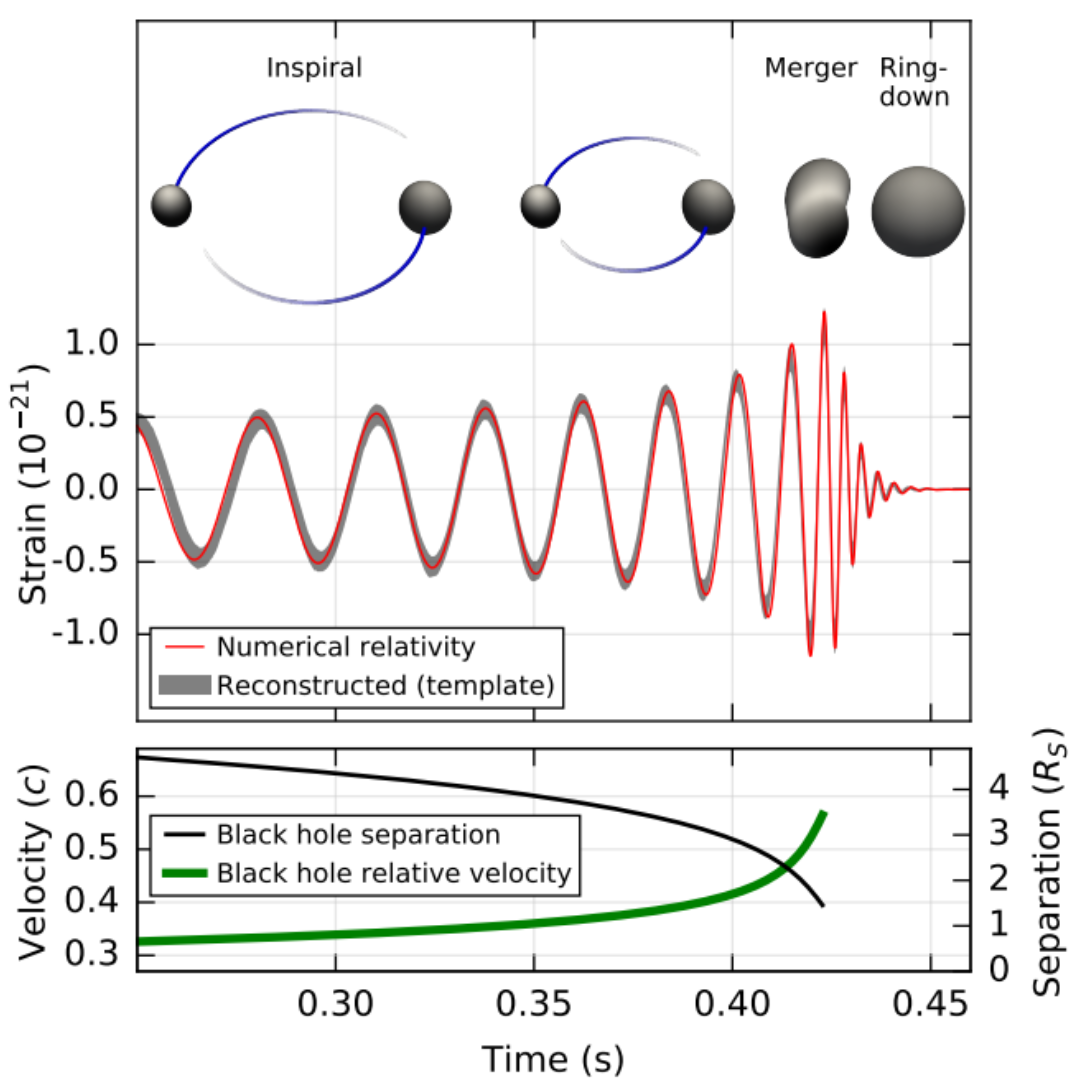
Figure 4. Images from a numerical relativity model (top), the gravitational wave strain (middle), and the relative velocity and separation of the black holes (bottom) for GW150914 over time. The very close separation of the two objects before merger (which is derived from the waveform) indicates that they are indeed black holes. Figure 2 of the detection paper.
The discovery of GW150914 represent results from the first month of advanced LIGO’s first observing run, which lasted a total of about 4 months. During this first month, another possible signal was found: LVT151012. Though much weaker than GW150914 and not significant enough to be declared a “detection,” it is likely astrophysical and from the coalescence of two black holes. From the detection of GW150914 and possible detection of LVT151012 during the first month, the possible rate of binary black hole mergers for systems analogous to these can be derived. If both GW150914 and LVT151012 are included, the rate of mergers for these classes of black holes is ~6–400 per cubic gigaparsec per year.
For almost all of humanity’s existence, the sole way in which we have studied our Universe is through light. This discovery has given us a new “sense” to explore the Universe, in a way opening our ears and allowing us to listen to the cosmos for the first time. Gravitational waves will allow us to probe objects, events, and epochs that are inaccessible to light, such as the merging of two black holes or the first second after the Big Bang. With more detections, we can further constrain the rate at which compact binary mergers occur, learn about the environments in which they occur, and test our models predicting their formation. Furthermore, when more advanced gravitational wave detectors join the network (such as advanced Virgo in late 2016), triangulation of gravitational wave sources in the sky will drastically improve, increasing the chances of detecting an electromagnetic counterpart to gravitational wave signals and probing these systems through multiple messengers. Needless to say, this detection will prove to be one of the most significant discoveries in modern physics, as it has opened an entire new realm of the Universe to explore.



Awesome write-up. Very exciting for astronomy!
“Note that we do not expect to see an electromagnetic counterpart for the merging of two black holes.” Any reason we can’t use light to detect this? Just the distance or interference?
Hi!
Black holes by their nature are…well “black”. They are so dense that not even light can escape their gravitational pull. When two black holes collide, even though this event is extremely energetic in gravitational waves, it would not emit a single photon. So nothing to “see” with traditional telescopes. (This isn’t the full story, as some people think we can see electromagnetic counterparts to binary black holes mergers if they have significant accretion disks…)
However, LIGO can also detect neutron star mergers, which have not yet accumulated enough mass to collapse into a black hole. If two neutron stars, or a neutron star-black hole binary were to merge, we could potentially see a bright explosion from the neutron-rich material or a gamma ray burst.
Thank you for the response! That makes sense and probably should have been a bit more obvious. I expect the upgrades that will be going on at LIGO over the next few years will help detection of the neutron star events you describe.
As a wanna-be astronomer (at least when I was a kid), I appreciate you explaining it at a level I can understand, even with my engineering differential equation math being rusty!
Similar to Dollar Flipper, and an extension: the immediate environment of the binary ~stellar-mass black holes (BHs) certainly includes at least a thin plasma (and some dust), possibly not so thin (or hot), depending on what was left of the events which created the BHs and/or the ‘birthplace’. With ~3 sols of gravitational wave radiation (GWR) ripping through this, would there have been any observable effects?
For example, suppose there was a solid planet, at a distance of 1 au (implausible, but bear with me), how would it have been affected by such energetic GWR squeezing/stretching it?
If the strain here on Earth was ~10^-21, at a distance of 1 km it would have been ~10^23 (10^9 light-years ~10^22 km), right (GWR energy is like EMR energy, declines as r^-2, right?)? So at 150 million km, ~4×10^6? I don’t really know what ‘strain’ is, in this case, nor if my BOTE calculation is ~OK, but it seems that’s far from trivial!
If there were accretion disks around the black holes, they would have likely been disrupted before black holes entered the LIGO frequency band, since the two black holes are only a few Schwarzschild radii apart when they enter the LIGO band.
It’s a really interesting question though to think about what the gravitational radiation from this event would do to nearby objects. It turns out that the gravitational wave strain goes as 1/r, not r^-2. Light intensity we measure in wave energy, which is proportional to the square of the wave amplitude. The light wave amplitude, however, drops off as 1/r. GW strain also drops off as 1/r.
The detectors we use to see EM radiation are sensitive to the energy EM waves carry, so they drop off as r^-2. However, for gravitational waves our detectors measure the wave amplitude directly (aka strain) and hence drop off as 1/r.
I did a quick back-of-the-envelope calculation for the scenario you mentioned above. A planet 1AU would be ~6 x 10^13 times closer than Earth is, which means the GW strain would be (6×10^13)*(1×10^-21) ~ 1e-7. If there were a LIGO on this planet, a strain of 1e-7 would mean a change of distance in the 4-km arms of ~.4 mm, which is comparable to the size of a grain of sand.
This would correlate to a 1e-7 pressure change. If this hypothetical planet had and atmospheric pressure of 1bar, this pressure change in the atmosphere would result in a sound intensity of ~50dB, which is similar to the sound intensity from an air conditioner. If the planet were instead a lunar distance away, the sound intensity would be 100dB (construction site).
Given that both a strong and a weak signal were detected in the first month. Should we expect these types of detections to occur at roughly a monthly rate? If true, that’s pretty exciting.
Even from just 1 detection, we can start to build rates at which merger events occur. If we just take the confirmed detection (GW150914), the rate at which mergers with similar properties to the black holes that created GW150914, is about 2-52 per Gpc^3 per year.
So, the short answer is yes. We do expect to see many more events, especially when the detectors get upgraded further and reach design sensitivity. But you never know!
Values given for the strain seem to be off: “a change in distance in the 4 kilometer-long arms that is a million times smaller than the size of a proton” is a strain of 5×10^-25, when the other example given: a change “as small as a hydrogen atom … ” over “an Earth-Sun distance” is a strain of about 7×10^-22. LIGO docs hope for “1/10,000th the width of a proton” which is a strain of 5×10^-23.
Whoops! You’re right, I meant to say 10,000 not 1 million. Thanks for the catch!
For a strain of ~10^-21:
LIGO’s 4-km arms can detect a change in distance ~10,000x smaller than the width of a proton
If the arms were ~1AU (150 million km), this strain would be a change in distance about the width of an atom
If the arms were ~4 lightyears (~distance to nearest star), this strain would be a change in distance about the width of a human hair
Hello
You correctly say “However, Einstein himself believed that any attempts to detect these “gravitational waves” would prove futile, as the effect that they have on their environment is miniscule. Almost poetically, a century after Einstein’s prediction this elusive phenomenon has been validated.”
The person who really works on this theory was Mileva Maric, she never had any doubt about her theory (and Einsteins’).
This texts is in Spanish, very is very important about her life: https://t.co/9fKo1VnjFQ. Yesterday was International Day of Women in Science. We should say HERstory too. 😉
Women have played a tremendous (and for a long time unappreciated) role in science. Particularly in astrophysics, from Caroline Herschel to Jocelyn Bell Burnell to Annie Jump Cannon. I’m not a historian, but I’ve heard there is a good deal of contention on whether Mileva Maric played any role in Einstein’s theories (other than being his wife during the time), though there is some evidence of her involvement.
This is indeed an exciting discovery. The article, however, would be even better if it discussed possible alternative sources of the detected signal (in addition to noise) and explained why gravitational waves from a merger of two black holes is the preferred explanation. At the moment the article explains that this is a result of numerical modeling but does not provide physical, qualitative arguments that would be easier for the readers to understand.
Hi Larry,
As these blogs are meant to be concise, it is impossible to touch on all the analyses of the discovery, especially since there were 12 papers in companion to the detection paper 🙂
If you’re interested in a somewhat brief overview, I’d recommend looking at fig. 4 of the detection paper and the surrounding text, available here: http://journals.aps.org/prl/pdf/10.1103/PhysRevLett.116.061102. Or feel free to ask me any specific questions.
For a more comprehensive description, the Detector Characterization, Calibration, Generic Transient Search, and Modeled Search companion papers would be good resources. Those are all available on arXiv.
Best,
Michael
Fermi (while pointing the wrong way) may have spotted something coincident: http://gammaray.nsstc.nasa.gov/gbm/publications/preprints/gbm_ligo_preprint.pdf
I saw this as well. Interesting, but given the huge sky area that GW150914 possibly originated from (~650 square degrees, which is the sky area of 2600 full moons), I personally doubt that the two events are related.
have you guys discovered/observed contraction or curving of spacetime or the gravitational waves?
Well, the effect that gravitational waves have is to contract and expand spacetime. So, I’d say the answer to both is yes 🙂
Hi Michael, hope it’s not too late to ask a question here
There’s one thing that’s still puzzling me: is the actual measured data proportional to the gravitational wave amplitude or to its intensity? As far as I understand, at least in a simplified picture, in the absence of GWs the MM interferometer is kept aligned so that light from both arms interferes destructively and no light reaches the photodetector. When a GW comes through, it produces a (tiny) phase difference that is proportional to the difference in arm lengths, hence to the GW amplitude. This results in light leaking onto the previously dark photodetector – the amplitude of this light again will be proportional to the amplitude of the GR wave. But since the photodetector measures light intensity, not light amplitude, won’t the measured signal be proportional to GW intensity?
Great question! The change in the interferometer arms is due to the amplitude of the GW (well…technically the projection of the GW amplitude on the plane of the detector). So the phase shift of the light is caused by the amplitude of the GW. In reality, the MM interferometers have Fabry-Perot cavities, so the laser beam bounces back and forth hundreds of times in the arms, building up a larger shift in its phase as a GW passes by.
You’re certainly correct about GW photodetector as well – they are sensitive to the intensity of the light signal, not the amplitude. So, we are using the intensity of the laser beam to measure the amplitude of the GW. However, it is the amplitude of the GW that affects the arms, and therefore it is the amplitude of the GW that affects the intensity of light that we see. So even though the photodetector is measuring the intensity of light, the measured signal is proportional to the GW amplitude.
Hope this makes sense!
OK, still not convinced – yes, the amplitude of the GW affects the arms (linearly), but the signal should be proportional to the square of the relative phase shift, hence to the square of the GW amplitude . Let me try some simplified calculations. If I’m getting it wrong, please point out where!
Output beam without GW: Acos(ωt) – Acos(ωt) = 0 (beams interfere, ω is light ang. frequency)
Output beam with GW: Acos(ωt) – Acos[ωt – bcos(νt)] (Now one beam has a phase shift oscillating at GW frequency; the amplitude b of this shift is given by d / λ, where d is the maximum difference in optical path (ie the difference in arm lengths) and λ the laser wavelength. Hence b is proportional to the GW amplitude)
Since b is very (very!) small, we can keep just the lowest-order (linear) term in b, so we get
Output beam with GW: A b sin(ωt) sin(νt)
But we measure the output beam intensity, hence proportional to b^2, hence GW intensity
I should correct – since, as you pointed out the lasers bounce back and forth – 400 times, as I seem to have read elsewhere – the difference in optical paths is actually 800 times the GW-induced difference in arm lengths. Right? But this doesn’t change the question.
This is an interesting question…and one I don’t think LIGO folk really consider (I’ll explain why in a second). Let me be explicit in my explanation and thought process, though to spoil the end result I believe that you’re correct that the intensity of light in the photodetector should scale as the square of the gravitational wave strain (i.e. scale as the “power” of the GW), but it is the amplitude of the gravitational wave itself that LIGO is “feeling”.
Let’s say the amplitude of the initial laser beam is given by A=E*sin(wt-kx), where E is the electric field and k is the wavenumber (2*pi/lambda). After hitting the beam splitter, identical lasers bounce in the cavities many times and eventually recombine (the average number of times the laser bounce is called the “finesse” (F)). Right before recombining, the amplitude of each beam is given by A = E/sqrt(2) sin(wt-2*F*k*L) where the L is the length of the unperturbed arm.
Now let’s imagine the arms have differing lengths, L1 & L2. By taking the superposition of the two beams, we can figure out the “intensity” of the beam by using some trig identities and by taking the time-average (since intensity is the average power transferred over one period of the wave). This is a standard result for the superposition of a beam with a Michelson-type interferometer: I = abs(E)^2 * sin^2(k(L1-L2)), where in our case (L1-L2) = 2*F*s*L0, where s is the gravitational wave strain, F is the finesse, and L0 is the rest length of the arms. By assuming the argument of sin^2() is small (which is valid for GW detection), you can taylor expand the for small values of L1-L2, and see that the first non-vanishing term in the series goes as the s^2 (the strain squared).
Now, this “intensity” represents the intensity of light at the interference fringes (not the total intensity of the laser light, which does not go to 0 when the arms are equal length). LIGO’s photodetector is set up at an interference minima (i.e. a dark spot on an interference pattern) when the arms are exactly the same length. When a gravitational wave passes by, this interference pattern shifts slightly, and the photodetector comes slightly out of the interference minima. It is this phase shift in the light that we care about, because the phase shift is directly proportional to the difference in arm length, the difference in arm length is directly proportional to the strain, and the strain is directly proportional to the gravitational wave amplitude. The phase shift is therefore the physically important quantity desired output of the photodetector, regardless if it is measuring intensity or not. If the photodetector does indeed measure the change in intensity, this quantity is converted to the physically important phase shift which is proportional to the gravitational wave amplitude.
So, all in all it is the gravitational wave amplitude that governs the change in length of LIGO’s arms and the phase shift in the interference pattern, though if we are just concerned about the intensity of the output beam I believe this would scale with the square of the amplitude (though I am still not 100% sure about this…I’ll ask around and let you know if I find something different). So, the relation between the strain and the data is just: data = R*strain where R is a “response function”, which hides all the mathematical transformations to relate different physics quantities.
Not sure if this is satisfying, but I think it is helpful to think of LIGO in relation to another instrument, such as a resistance-temperature detector (RTD). The goal of the RTD is to measure temperature. However, what it actually measures is a voltage, which is converted into a resistance via Ohm’s law, which is converted into a temperature by some functional relation between temperature and resistance. Same idea with LIGO. We want to measure the change in length of the arms (or the strain, or the GW amplitude) because this is the physical change in the interferometer. However, to do so we need to make some kind of a measurement on light (be it intensity or phase shift) and use some functional relationship to determine the strain.
I’ll let you know if I can think of a better, more intuitive way to answer this question…